Управление капиталом
14.1. Введение.
Управление капиталом - это набор правил, определяющих объем открываемых позиций в момент поступления соответствующих сигналов от механической торговой системы. Так как метод управления капиталом непосредственно влияет на динамику торгового счета, то при его выборе нужно четко определить свои инвестиционные цели.
Технически задача сводится к тому, чтобы задать такой алгоритм вычисления доли участвующего в конкретной сделке капитала, чтобы максимизировать один из показателей динамики торгового счета. Этими показателями могут быть средний доход на одну сделку, соотношение дохода и риска сделок, средний прирост торгового счета по фиксированным промежуткам времени (например по месяцам) и т.д.
Как и торговая система, метод управления капиталом должен быть тщательным образом протестирован. При этом требования к нему схожи с требованиями к торговой системе:
- небольшое количество оптимизируемых параметров,
- устойчивость в области оптимальности параметров,
- должно существовать по крайней мере несколько активов, на которых совокупность из торговой системы и метода управления капиталом имеет удовлетворительные результаты без повторной оптимизации.
14.2. Ограничение суммы убытка в сделке.
Пусть торговая система дала сигнал о покупке актива по цене enter price, причем величина риска по сделке составляет %risk, то есть в случае движения против открытой позиции сделка должна быть закрыта по цене exit price = enter price x (1 - %risk) .
Рассмотрим вопрос о том, как выбрать долю участвующего в сделке капитала таким образом, чтобы в случае неблагоприятного развития ситуации убыток не превысил заранее заданного значения. Размер капитала до и после проигрышной сделки и величина максимального убытка (в деньгах) связаны соотношением
max net loss = exit equity - enter equity
Обозначим как a долю участвующего в сделке капитала, причем 0 < a < 1. Тогда количество покупаемых ценных бумаг (лотов) равно
, ax enter equity
volume =-
i—--
enter price x (1 + % comission)
После закрытия сделки величина капитала будет равна exit equity = (1 - a) x enter equity +
+ exit price x (1 - % comission) x volume
Подставляя в последнюю формулу написанные ранее соотношения после несложных преобразований получаем выражение для доли участвующего в сделке капитала
| max net loss | 1 + % comission
a =-x-
enter equity 2 x % comission + %risk x (1 - % comission)
При определенном соотношении между enter equity ,
max net loss и %risk вычисленная по этой формуле величина a
может оказаться больше 1. В этом случае в данной сделке участвует весь капитал. Выражение для количества покупаемых бумаг (лотов) имеет вид
с
volume = ЦЕЛОЕ
a x enter equity
enter price x (1 + % comission)
y
Данный метод управления капиталом имеет очень простой смысл - ограничить предельно допустимый убыток по конкретной сделке не ограничивая при этом возможную прибыль. Оптимизация метода проводится по величине предельно допустимого убытка max net loss .
Основным недостатком этого метода является отсутствие адаптации к текущей величине торгового счета. При существенном изменении капитала относительно начальных инвестиций величину предельно допустимого убытка нужно пересматривать и заново оптимизировать.
14.3. Ограничение процента убытка в сделке.
В отличие от рассмотренного в предыдущем параграфе, метод риска фиксированным процентом капитала в каждой сделке
205
автоматически адаптируется к текущей величине торгового счета.
Размер капитала до и после проигрышной сделки и величина максимального убытка (в %) связаны соотношением
.. , exit equity
max % loss =--1
enter equity
Проведя выкладки, аналогичные сделанным в предыдущем параграфе, можно получить выражение для доли участвующего в сделке капитала
. , . 1 + % comission
a =| max % loss | x-
2 x % comission + %risk x (1 - % comission)
При определенном соотношении между max % loss и %risk вычисленная по этой формуле величина a может оказаться больше 1. В этом случае в данной сделке участвует весь капитал. Выражение для количества покупаемых бумаг (лотов) имеет вид
с
volume = ЦЕЛОЕ
a x enter equity
enter price x (1 + % comission)
J
Этот метод позволяет автоматически реинвестировать прибыль выигрышной МТС. С другой стороны, в случае попадания в полосу убыточности, величина предельно допустимых потерь в денежном выражении постоянно уменьшается после каждой проигрышной сделки.
14.4. Максимизация средней величины дохода МТС.
Рассмотрим формулу для вычисления среднего значения дохода сделок (в %) для случая, когда в каждой сделке участвует весь капитал:
\ 1/ total trades
i total trades \
avg % profit
П
(1 + %P
rofit (i))
V i=1 J
Если в каждой сделке участвует только доля капитала a, причем 0 < a < 1, и эта доля одинакова для всех сделок, то
1 / total trades
С total trades
avg % profit (a)
П(1 + a x % profit (i))
V i=1
206
В отдельных случаях выбором соответствующего значения a можно максимизировать величину avg % profit (a) так, чтобы avg % profit (a) > avg % profit.
В общем случае для произвольной последовательности сделок задача решается численно путем перебора всех значений a с небольшим шагом изменения (например 0.01). Однако, так как эта операция достаточно трудоемка, то хотелось бы найти простые характеристики торговых систем, которые бы определяли возможность такой оптимизации.
Вернемся к формуле среднего значения дохода сделок. Ее можно записать, используя средние значения выигрышных и проигрышных сделок, а также процент выигрышных сделок для случая, когда в каждой сделке участвует весь капитал:
1 + avg % profit =
= (1 + avg %win)
wm trades% x (1- | avg %loss |)
1-win trades%
Будем приближенно считать, что 1 + avg % profit (a) *
* (1 + a x avg %win)
wm trades% x (1 -ax | avg %loss |)
1-win trades%
Последнее равенство не является строгим, однако для оно вполне пригодно для оценочных вычислений оптимальной величины a .
Введем функцию S (a) = ln(1 + avg % profit (a)) . Так как натуральный логарифм является монотонно возрастающей функцией, то максимум функции S (a) соответствует максимуму функции avg % profit (a) .
Запишем S (a) в явном виде:
S (a) = win trades % x ln(1 + a x avg %win) +
+ (1 - win trades %) x ln(1 -ax | avg %loss |)
Возьмем производную S(a) по a :
dS(a) win trades% x avg %win (1 - win trades%)x | avg %loss | da 1 + ax avg %win 1 -ax | avg %loss |
Приравняв производную к нулю, получим формулу для вычисления оптимального значения a (в том случае, если экстремум существует):
207 win trades % x avg %win - (1 - win trades %)x | avg %loss | avg %win x | avg %loss |
a =¦
opt
Так как a
opt > 0 то win trades % > win trades % min
где
... . | avg %loss |
win trades % min =-
avg %win + | avg %loss |
Если последнее неравенство не соблюдается, то экстремума не существует и a
opt = 0, то есть по такой МТС торговать нельзя.
Так как a
opt < 1, то win trades % < win trades % max где
| avg %loss |
win trades % max = -
— (1 + avg %win ) avg %win +1 avg %loss |
Если последнее неравенство не соблюдается, то экстремума не
существует и a
opt = 1, то есть по такой МТС нужно торговать
всем капиталом в каждой сделке.
Приведем несколько примеров решения задачи оптимизации доходности МТС.
Неоптимизируемая система с положительным математическим ожиданием дохода
Результаты тестирования МТС: win trades % = 50%
avg %win = 15% avg %loss = -10%
Неоптимизированная прибыль на сделку: avg % profit = 1.73%
Границы области оптимизации:
win trades % min = 40% win trades % max = 46%
Так как win trades % > win trades % max, то функция avg % profit (a) не имеет экстремума и монотонно возрастает при увеличении a .
208
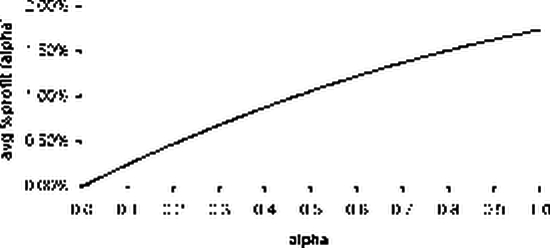
По такой МТС нужно торговать всем капиталом в каждой сделке.
Неоптимизируемая система с отрицательным математическим ожиданием дохода
Результаты тестирования МТС: win trades % = 35%
avg %win = 15% avg %loss = -10%
Неоптимизированная прибыль на сделку: avg % profit = -1.94%
Границы области оптимизации:
win trades % min = 40% win trades % max = 46%
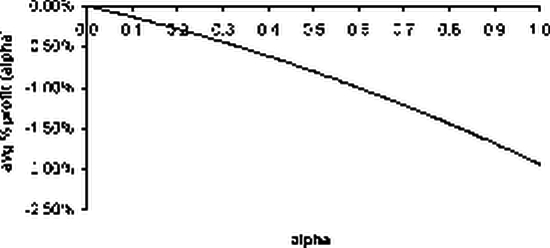
Так как win trades % < win trades % min, то функция avg % profit (а) не имеет экстремума и монотонно убывает при увеличении а . По такой МТС торговать нельзя.
209
Оптимизируемая система с положительным математическим ожиданием дохода
Результаты тестирования МТС: win trades % = 44%
avg %win = 15% avg %loss = -10%
Неоптимизированная прибыль на сделку: avg % profit = 0.25%
Границы области оптимизации:
win trades % min = 40% win trades % max = 46%
В данном случае возможна оптимизация системы, так как win trades % min < win trades % < win trades % max . Функция avg % profit (а) имеет экстремум в точке
a
opt = 0.67, при этом avg % profit (а
t) = 0.33% .
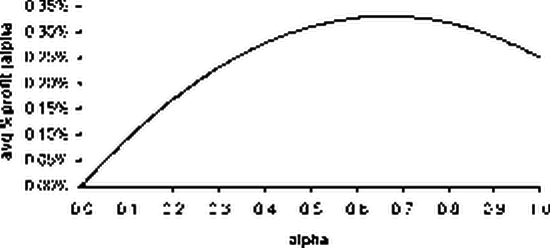
Мы получили, что в результате оптимизации повышается доходность прибыльной системы.
Оптимизируемая система с отрицательным математическим ожиданием дохода
Результаты тестирования МТС: win trades % = 42.5%
avg %win = 15% avg %loss = -10%
Неоптимизированная прибыль на сделку: avg % profit = -0.12%
Границы области оптимизации:
210
win trades % min = 40% win trades % max = 46%
В данном случае возможна оптимизация системы, так как win trades % min < win trades % < win trades % max . Функция avg % profit (a) имеет экстремум в точке
a
opt = 0.42, при этом avg % profit (a
t) = 0.13% .
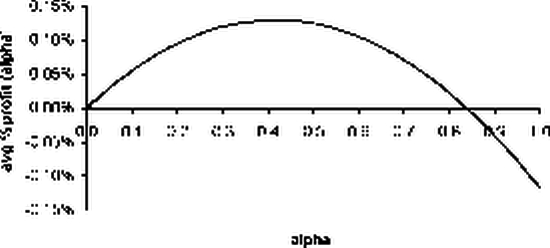
Мы получили, что в результате оптимизации убыточная система становится прибыльной.
14.5. Оптимизация соотношения дохода и риска МТС.
Для оптимизации соотношения дохода и риска МТС нужно найти такую долю a участвующего в сделке капитала, которая максимизировала бы следующую функцию:
Q (a) = (1 + a х avg %win)
wm trades % x
x (1 -ax | avg %loss |)
1-win trades % x (1 -ax %risk) -1
В данной формуле %risk - это один из показателей риска МТС, который в зависимости от предпочтений конкретного трейдера может принимать, например, следующие значения:
% risk = stdev % profit
% risk =| avg % drawdown |
% risk =| max % drawdown |
Перейдем к функции S(a) = ln(1 + Q(a)), экстремум которой, если он существует, совпадает с экстремумом Q(a) .
211
S (a) = win trades % x ln(1 + ax avg %win) +
+ (1 - win trades %) х ln(1 -ax | avg %loss |) + (1 -ax %risk) Взяв производную S(a) по a и приравняв ее к нулю получим:
aopt =
a
1 -у]af - 4a
0a
2
2a
2
где
a
0 = win trades% x avg %win - (1 - win trades%) x | avg %loss | -
- %risk
a
1 = avg %win x (%risk +1 avg %loss |) +
+ win trades% x %risk x (avg %win +1 avg %loss |) -
- 2 x %risk x | avg %loss |
a
2 = 2 x avg %win x | avg %loss | x %risk
Так как a
opt > 0 то win trades % > win trades % min где
win trades % min = ¦
%risk + | avg %loss | avg %win + | avg %loss |
opt
Так как a
p < 1, то win trades % < win trades % max
где
win trades % max
%risk + | avg %loss | -2 x %risk x | avg %loss | avg %win + | avg %loss |
1 + avg %win 1 - %risk
Если не соблюдается двойное неравенство
win trades % min < win trades % < win trades % max, то экстремума не существует, то есть по данной методике нельзя формальным образом выбрать наилучшее соотношение дохода и риска.
Приведем пример решения задачи оптимизации соотношения доходности и риска МТС.
Результаты тестирования МТС:
212
win trades % = 64% avg %win = 15% avg %loss = -5%
Неоптимизированная прибыль на сделку: avg % profit = 7.36%
Принятая величина риска:
%risk = 7%
Найдем показатели, характеризующие соотношение дохода и риска до оптимизации:
(1 + avg % profit) х (1 - %risk) -1 =
= (1 + 0.0736) х (1 - 0.07) -1 = -0.0016
avg %p
rofit = 736 =
1 0509 %risk 7
Границы области оптимизации: win trades % min = 60%
win trades % max = 70%
В данном случае возможна оптимизация системы, так как win trades % min < win trades % < win trades % max .
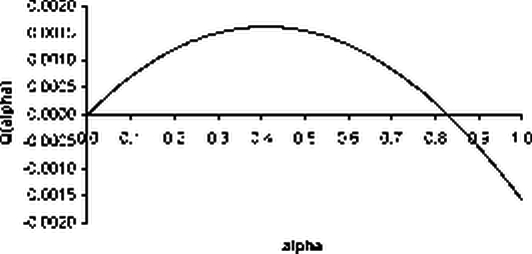
Функция Q (а) имеет экстремум в точке GC
opt = 0.41, при этом
avg % profit (a op
t) = 3.12%,
%risk (a
opt) = %risk х a
opt = 7% х 0.41 = 2.87%
|
213
|
Соотношения дохода и риска после оптимизации:
Q
(aopt
) =
(1 +
avg %Р
ГФ
(aopt))
Х (1 - %
risk (aopt))
- 1 =
= (1 + 0.0312) х (1 - 0.0287) -1 = 0.0016
avg % profit
(aop
t) 3.12
= 1.0878
2.87
%risk
(aopt
)
Как видно из полученных результатов, после оптимизации довольно существенно снизился доход на одну сделку, однако улучшились соотношения дохода и риска. Кроме того, небольшая величина доли капитала, участвующего в сделках, позволяет чувствовать себя более комфортно на волатильных рынках.
14.6. Анализ соотношения скользящих средних от кумулятивной кривой дохода сделок.
В предыдущих параграфах рассматривались методы оптимизации доли участвующего в сделках капитала в зависимости от показателей МТС (процента прибыльных сделок, средней величины выигрыша, средней величины проигрыша). Однако, не была учтена возможность корреляции между результатами последовательных сделок, то есть возможность возникновения серий из прибыльных или убыточных сделок.
Формально, наличие корреляции в доходах сделок можно выявить, найдя коэффициент автокорреляции динамического ряда % profit (trade number) , где trade number - номер сделки, % profit - величина дохода по данной сделке (%). После этого нужно проверить гипотезу о том, значимо ли отличается вычисленная по выборке величина коэффициента автокорреляции от нуля.
Высокая положительная корреляция свидетельствует о том, что за выигрышем чаще следует очередной выигрыш и реже следует проигрыш и наоборот. При высокой отрицательной корреляции за выигрышем чаще следует проигрыш и реже - очередной выигрыш и наоборот.
Наличие корреляции между результатами сделок можно использовать в торговле двумя способами. Во-первых, модификацией решающих правил торговой системы, однако это может привести к ее излишнему переусложнению. Во-вторых, использованием методов управления капиталом, что представляется более предпочтительным. Как правило, если корреляция присутствует, то она по
214
ложительна, следовательно возможны достаточно длинные серии из прибыльных или убыточных сделок. Очевидно, что в полосе прибыльности нужно увеличивать долю участвующего в сделке капитала, а в полосе убыточности - уменьшать.
При наличии высокой положительной корреляции доходов сделок очень простым и достаточно эффективным способом управления величиной участвующего в сделке капитала является метод, основанный на соотношении скользящих средних различных порядков от размера торгового счета после каждой сделки exit equity (trade number) .
Обозначим как short line и long line короткую и длинную простую скользящую среднюю от величины exit equity .
Если short line > long line , то в среднем в настоящее время торговая система показывает лучшие результаты, чем в среднем в прошлом. Следовательно, система находится а полосе прибыльности и нужно увеличивать объемы сделок. Самое простое решение - участвовать всем капиталом в каждой сделке.
Если short line < long line , то в среднем в настоящее время торговая система показывает худшие результаты, чем в среднем в прошлом. Следовательно, система находится а полосе убыточности и нужно уменьшать объемы сделок. Самое простое решение - вообще не открывать позиции.
Однако, возможны ситуации, когда единственная не проведенная прибыльная сделка по упущенной выгоде перекрывает экономию от нескольких не проведенных убыточных сделок. Для исключения таких случаев можно предложить следующую методику:
1) Рассчитаем набор случайных величин {x
k } где x = \n(short line / long line) .
2) По полученной выборке найдем оценки среднего значения и с.к.о. величины x. Так как эти величины должны пересчитываться после каждой закрытой сделки, то обозначим их
как X
k и и
к .
3) Если приближенно считать, что случайная величина x подчиняется нормальному распределению, то в качестве доли
215
участвующего в очередной сделке капитала можно выбрать значение интегральной функции распределения в последней перед планируемой сделкой точке выборки. Используя функции Microsoft Excel можно найти долю капитала по формуле:
a
k+
1 = НОРМСТРАСП
X - -г,
Л
\
ak )
Возможны следующие варианты
|
xk << Xk
|
|
ak+1 * 0
|
xk < Xk
|
|
0 <ak+1 < 0.5
|
Xk = Xk
|
|
ak+1 = °-5
|
Xk > Xk
|
|
°-5 <ak+1 <1
|
Xk >> Xk
|
|
ak+1 *1
|
|
Таким образом, при short line = long line доля участвующего в сделке капитала будет равна 50%, при short line > long line доля будет возрастать от 50% вплоть до 100%, а при short line < long line доля будет уменьшаться от
50% вплоть до 0%.
Метод управления капиталом по соотношению скользящих средних может может быть оптимизирован по двум параметрам: периоду короткой скользящей средней и периоду длинной скользящей средней.
14.7. Критерий серий.
Одним из важнейших показателей механической торговой системы является доля выигрышных сделок win trades % . Однако, эта величина никак не характеризует наличие или отсутствие корреляции между результатами сделок. Возможны следующие варианты:
1) Исходы последовательных сделок независимы друг от друга, то есть выигрыши и проигрыши чередуются случайным образом. В этом случае мы имеем нулевую корреляцию между результатами сделок.
216
2) За выигрышем чаще следует выигрыш, за проигрышем -проигрыш, то есть возникают полосы прибыльности и убыточности. В этом случае мы имеем положительную корреляцию между результатами сделок.
3) За выигрышем чаще следует проигрыш, за проигрышем -выигрыш. В этом случае мы имеем отрицательную корреляцию между результатами сделок
Рассмотрим результаты последовательных сделок торговой системы. Назовем серией несколько следующих подряд прибыльных сделок или несколько следующих подряд убыточных сделок. В случае положительной корреляции количество серий на периоде тестирования будет меньше, чем количество серий при независимом чередовании прибылей и убытков. При отрицательной корреляции ситуация будет обратной. Заметим, что при расчете серий учитывается только знак дохода по сделке, а не его абсолютная величина, при этом сделки с нулевым доходом учитываются как убыточные.
Критерий серий позволяет определить, насколько значимо отличие полученного по выборке сделок эмпирического значения числа серий от ожидаемого числа серий при независимом распределении прибылей и убытков. Введем обозначения:
N - количество сделок (N = total trades). p - вероятность прибыльной сделки (p = win trades %).
R - эмпирическое значение числа серий по выборке сделок.
При достаточно большом N (больше 50) и при отсутствии корреляции между результатами сделок случайная величина R будет подчиняться нормальному распределению с параметрами:
2p(1 — p)N - ожидаемое значение числа серий.
2p(1 — p)4N - с.к . о. числа серий.
Для приведения случайной величины R к стандартному виду (то есть к величине с нулевым математическим ожиданием и единичной дисперсией) нужно сделать преобразование
Z = R - 2p(1 - p)N 2 p(1 - p)4n
Полученную таким образом нормированную случайную величину называют Z -счетом. Положительный Z -счет возника
217
ет, если количество серий больше ожидаемого, то есть при отрицательной корреляции. Отрицательный Z -счет возникает, если количество серий меньше ожидаемого, то есть при положительной корреляции.
Вероятность того, что стандартная нормальная величина находится в интервале от — | Z | до | Z |, или соответствующую величине Z -счета доверительную вероятность, можно вычислить с помощью таблиц Microsoft Excel: P(Z) = 2 • НОРМСТРАСПЦ Z |) — 1.
Как правило считают, что при | Z |< 1.96 (P(Z) < 95%), отклонение эмпирического числа серий от ожидаемого незначимо и объясняется случайностью выборки. В этом случае нецелесообразно модифицировать торговую стратегию на основании Z -счета.
Если же мы имеем систему, у которой | Z |> 1.96 (P(Z ) > 95% ), то можно использовать полученную закономерность следующим образом:
1) При большом по модулю и положительном по знаку Z -счете за прибыльной сделкой скорее всего последует убыточная, а за убыточной - прибыльная. Следовательно, после выигрышей нужно уменьшать объем следующей сделки, а после проигрышей - увеличивать.
2) При большом по модулю и отрицательном по знаку Z -счете за прибыльной сделкой скорее всего последует очередная прибыльная сделка, а за убыточной - очередная убыточная. Следовательно, после выигрышей нужно увеличивать объем следующей сделки, а после проигрышей - уменьшать.
Отметим, что критерий серий может служить фильтром для рассмотренного в предыдущем параграфе метода скользящих средних.
14.8. Увеличение объема выигрывающей позиции.
В этом параграфе будет изложен метод увеличения объема выигрывающей длинной позиции для трендовых систем. Как правило такие торговые системы имеют сравнительно небольшой процент выигрышных сделок и высокое отношение средней прибыли к среднему убытку.
218
Пусть торговая система дала сигнал о покупке актива в момент времени t
1 по цене Р
1 . В этом случае проводится первая покупка, причем сумма сделки равна а процентов от текущей величины свободных денежных средств. Если цена продолжает рост, то в момент времени 1
2 делается вторая покупка по цене Р
2 на сумму а
2 процентов от текущей величины свободных
денежных средств. Наращивание объема бумаг продолжается до тех пор, пока растет рыночная цена. Заметим, что начиная со второй сделки средняя цена покупки меньше текущей цены актива. При развороте рынка и достижении ценой некоторого критического уровня все позиции закрываются.
Изложим эту методику формальным образом. Введем обозначения:
X
0 - начальная величина свободных денежных средств,
N - общее число проведенных сделок,
Р
к - цена, по которой проводится к -я сделка (рыночная цена), c - комиссия за проведение сделки (%),
X
N - величина свободных денежных средств после N сделок,
YN
b'
) - общие затраты на покупку после N сделок (балансовая стоимость бумаг),
V
N - количество бумаг в портфеле после N сделок,
PN
B - средняя цена покупки актива после N сделок (балансовая цена).
После проведения N сделок, где сумма к -й сделки составляет а
к процентов от текущей величины свободных денежных
средств, перечисленные выше переменные будут выражаться формулами:
N
Xn = X 0-П (1 -ак)
к=1
1
-П
(1 -ак
)
Y (B)
N
X0
X0 - XN
к=1
219
k-1
V =
ху N
I а'П(1 -а)
\
Гк г =1
1 +
c k=1 Pi.
i
-П
(1 -ak
)
Y ( B)
P= -
V- = (1 + c) ¦
V AT
k=1
k-1
k=1 V
Pk г=1
Для последующих рассуждений эти формулы нужно разумным образом упростить. Сделаем два допущения:
1) Все a
k одинаковы и равны a .
2) Все покупки, начиная со второй, происходят при определенном процентном приросте рыночной цены относительно цены предыдущей сделки, то есть
Pk = P • (1 + в)
k 1
После этих упрощений формулы примут вид:
Xn = X0 • (1 -a)
N
YN
b) = X„ '(1 - (1 -a)
N)
OC'X,
1 + в
P • (1 + c) a + в
1 -a
1-
VN =
1 a + в 1 - (1 - a)
N
PN
b) = P'(1+c)'-'
1-
1+в
Рассмотрим зависимость этих переменных от количества сделок N на примере. Примем следующие значения входящих в формулы параметров:
a = 30% в = 5% c = 0.2%
P1 =1
х
0 = 100 000
Результаты расчетов с этими значениями параметров приведены в таблице:
220
N
|
1
|
2
|
3
|
4
|
5
|
Pn
|
1.000
|
1.050
|
1.103
|
1.158
|
1.216
|
Xn
|
70 000
|
49 000
|
34 300
|
24 010
|
16 807
|
Y (B)
7n
|
30 000
|
51 000
|
65 700
|
75 990
|
83 193
|
Vn
|
29 940
|
49 900
|
63 207
|
72 078
|
77 992
|
P ( B)
J N
|
1.002
|
1.022
|
1.039
|
1.054
|
1.067
|
При работе по такой методике закрытие позиций может осуществляться следующим образом:
1) Если после первой сделки рынок пошел против открытой позиции, то выход осуществляется по сигналу stop loss, причем так как объем сделки сравнительно невелик, то убыток будет небольшим.
2) После второй сделки цену выхода можно поставить на границу
безубыточности (с учетом комиссии), то есть
p(
exlt) = р(В) /(1 _
С).
Для данного примера P
2(ext) = 1.0022/(1 _ 0.002) = 1.024.
После второй сделки, если не произойдут форс-мажорные события, портфель застрахован от убытков при неограниченном потенциале прибыли.
3) Начиная с третьей сделки цена выхода может равняться цене входа для предыдущей сделки. Например, цена выхода после пятой сделки равна цене входа по четвертой сделке, то есть 1.158, при этом средняя цена покупки с учетом комиссии равна 1.067.
Если открытие позиций осуществляется частями, то выход происходит всем объемом единовременно. Выход частями может быть целесообразен только в случае, когда разница между текущей рыночной ценой и средней ценой покупки достаточно велика, то есть если входы были сделаны на сильном и продолжительном восходящем тренде.
Содержание раздела




