Механические торговые системы
13.1. Введение.
Определим инвестирование как вложение свободных денежных средств в различные виды финансовых активов с целью получения прибыли. При формировании инвестиционного портфеля выбирается такой набор активов и такой способ управления ими, которые бы обеспечивали ожидаемый доход не ниже заранее заданного минимального значения при риске получения дохода не выше заранее заданного максимального значения. Существуют два основных способа управления портфелем ценных бумаг: активный и пассивный.
Суть пассивного управления состоит в создании хорошо диверсифицированного, состоящего из большого количества активов портфеля, и продолжительного удерживания его в неизменном состоянии. Пассивный портфель характеризуется низким оборотом и малым уровнем накладных расходов.
Мы сконцентрируем внимание на рассмотрении активного управления портфелем, которое нацелено на получение дохода выше среднерыночного уровня. Активное управление подразумевает:
- выбор небольшого количества высоколиквидных активов для формирования портфеля,
- определение правил открытия и закрытия позиций по каждому из активов,
- определение объема открываемых позиций,
- оптимизацию портфеля, то есть методы снижения рисков. Определим некоторые понятия, которые будем использовать
в дальнейшем.
Механическая торговая система (МТС) - набор правил, однозначно определяющих моменты открытия и закрытия позиций, то есть МТС задает правила входа в позицию, правила выхода из выигрывающей позиции, правила выхода из проигрывающей позиции.
Управление капиталом - набор правил, определяющих объем открываемых позиций в момент поступления соответствующих сигналов от МТС.
Оптимизация портфеля - методы, позволяющие выбрать такой состав портфеля активов и торгующих эти активы механических систем, которые бы в наибольшей степени соответствовали инвестиционным предпочтениям конкретного трейдера.
13.2. Механический и интуитивный подход к торговле.
Динамику биржевых цен активов можно представить как стохастический и нестационарный процесс. Однако, это не исключает возможность нахождения такого набора эмпирических правил, что проведение в соответствии с ними торговых операций позволяет увеличить доходность и/или уменьшить риск вложения в данный актив по сравнению с пассивной стратегией "купил и держи".
Создание механической торговой системы - это полная формализация таких правил. При этом нужно понимать, что так как правила открытия и закрытия позиций разрабатываются на основе прошлой истории цен, то не существует гарантии того, что МТС на их основе будет успешно работать и в будущем. Но чем более качественно проведено тестирование МТС, тем больше оснований надеяться на то, что ее результаты при реальной торговле будут находиться в приемлемых для трейдера пределах.
У механического подхода есть два преимущества по сравнению с часто практикуемым интуитивным подходом к торговле:
- при принятии торговых решений исключается эмоциональный фактор,
- принятые торговые решения не являются субъективными, следовательно оправдано формальное статистическое исследование результатов работы МТС, позволяющее найти и скорректировать ее слабые места.
Следует еще раз подчеркнуть, что для любой механической системы существует вероятность того, что по истечении любого интервала времени в результате проведения торговых операций по ее сигналам будет получен убыток. Однако, для достаточно хорошей системы эта вероятность тем меньше, чем больше время торговли. Поэтому считается, что для того, чтобы МТС смогла реализовать свое статистическое преимущество, необходимо не менее 2-3 лет.
177
13.3. Свойства МТС.
Показатели механической торговой системы характеризуют результаты ее работы. Величина, разброс и устойчивость показателей определяют качество системы. Подробно показатели МТС и методы их статистического исследования будут рассмотрены ниже.
Параметрами механической торговой системы называются переменные, присутствующие в правилах открытия и закрытия позиций. В результате тестирования и оптимизации МТС определяется такой набор параметров, при котором величина, разброс и устойчивость важнейших показателей системы находятся в оптимальных для конкретного трейдера пределах. Хорошая МТС должна обладать следующими свойствами:
- иметь небольшое количество оптимизируемых параметров,
- иметь удовлетворительные показатели работы при реальных рыночных комиссиях,
- обладать устойчивостью показателей работы в области оптимальности параметров,
- должно существовать по крайней мере несколько активов, на которых система имеет приемлемые результаты без повторной оптимизации.
Число оптимизируемых параметров
Чем больше оптимизируемых параметров имеет МТС, тем меньше вероятность того, что она будет удовлетворительно работать при реальной торговле. Это связано с тем, что при большом числе параметров система подгоняется под исторический ряд цен, на котором происходило тестирование. Но ряды цен активов в большой степени носят случайный характер. Задачей же хорошей системы является не учет всех особенностей конкретной случайной выборки, а выявление более или менее постоянно действующих на рынке закономерностей. Здесь уместна аналогия с регрессионным анализом, где также нужно с осторожностью относиться к излишнему переусложнению модели.
Величина комиссии
Важным моментом при тестировании МТС является величина комиссии, которая должна соответствовать реальным на
178
кладным расходам при совершении сделки, то есть она должна учитывать следующие величины:
- комиссию с оборота (брокерскую и биржевую),
- спрэд (разницу между котировками на покупку и продажу),
- проскальзывание (разницу между величиной сигнала МТС и реальной ценой исполнения сделки).
Если биржевая и брокерская комиссии не зависят от вида актива, то на величины спрэдов и проскальзываний существенное влияние оказывает ликвидность конкретного актива. В целом можно сказать, что при тестировании МТС суммарную комиссию следует выбирать не менее чем 0.5% от суммы сделки даже для наиболее ликвидных активов.
Устойчивость показателей в области оптимальности
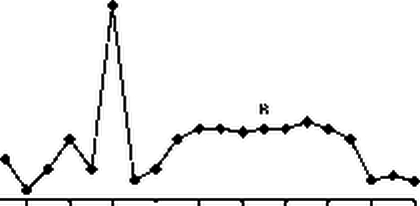
Устойчивость показателей МТС в области оптимальности параметров проще всего проиллюстрировать графически для системы, зависящей от единственного параметра. Рассмотрим график зависимости одного из показателей системы (доходности в % годовых) от величины оптимизируемого параметра.
|
А |
 |
|
2 4 6 8 10 12 14 16 18 20 Параметр |
90% -80% -л 70% -
g 60% -
Ч 50% -° 40% -
п 30% -20% -10%
0%
0
В данном случае выбор в качестве оптимальной величины параметра значение, соответствующее точке А (параметр=6, доход-ность«95%год.), не является правильным, так как в районе этой точки величина доходности является неустойчивой и столь резкий пик вероятнее всего объясняется особенностями конкретной случайной выборки, на которой происходило тестирование.
179
Более разумным представляется выбор в качестве оптимальной величины параметра значение, соответствующее точке В (пара-метр=13, доходность«35%год.), так как в области этой точки доходность устойчива к изменению параметра в достаточно широких пределах.
На устойчивость следует проверять все важные для трейдера показатели работы системы. У разных показателей области устойчивости будут вообще говоря разными. В качестве оптимального следует выбрать такое значение параметра, которое находится в области устойчивости большинства наиболее важных для трейдера показателей системы.
Удовлетворительные результаты на различных активах
Механическая система как правило создается, тестируется и оптимизируется на историческом ряде цен одного актива. Одной из главных задач создания хорошей МТС является предотвращение ее подгонки под конкретные исторические данные, которые наверняка не повторятся в будущем. Эффективным способом проверки МТС на излишнюю подгонку является переход на другие активы без изменения параметров системы. Если при переходе на исторические ряды цен других активов без повторной оптимизации параметров система продолжает показывать удовлетворительные результаты, то это повышает вероятность того, что она окажется прибыльной в реальной торговле. При этом надо иметь в виду, что если активы высококоррелированы, то это существенно снижает ценность такой проверки. Если же при переходе с ряда цен исходного актива (на котором МТС создавалась и оптимизировалась) на ряд цен высококоррелированного с ним актива система разваливается, то это служит веским основанием для отказа от нее.
13.4. Минимальное число сделок.
Для достоверной оценки величины и разброса показателей механической торговой системы количество сделок на периоде тестирования не должно быть меньше некоторого минимального значения. Считая, что результат отдельной сделки (например размер прибыли) является случайной величиной, оценим минимальный объем выборки для идентификации закона распределения этой величины. Для идентификации закона распределения необходимо построить гистограмму эмпирических частот и провести сравнение эмпирических и теоретических частот по критерию хи-квадрат.
180
Напомним, что минимальное количество столбцов гистограммы должно равняться пяти.
Так как приводимые ниже выкладки будут носить оценочный характер, предположим заранее, что исследуемая случайная величина подчиняется нормальному закону распределения.
Примем в качестве интервала возможных значений этой величины промежуток (р — 2о, р + 2о). Вероятность оказаться внутри этого интервала 95.45%. Ширину столбца гистограммы можно найти, разделив ширину интервала возможных значений, то есть 4о , на минимальное количество столбцов гистограммы, то есть число 5. В итоге получим, что ширина столбца равна 0.8о . В таблице приведены значения нормированных теоретических частот попадания в соответствующие столбцы гистограммы для стандартной нормальной величины (р = 0, о = 1) .
|
Номер интервала Левая граница |
Правая граница |
Нормированная частота | |
|
1 |
-2.0 |
-1.2 |
0.0923 |
|
2 |
-1.2 |
-0.4 |
0.2295 |
|
3 |
-0.4 |
0.4 |
0.3108 |
|
4 |
0.4 |
1.2 |
0.2295 |
|
5 |
1.2 |
2.0 |
0.0923 |
|
|
|
ИТОГО |
0.9545 |
Номер интервала Левая граница Правая граница Частота
|
1 |
-2.0 |
-1.2 |
5 |
|
2 |
-1.2 |
-0.4 |
12 |
|
3 |
-0.4 |
0.4 |
17 |
|
4 |
0.4 |
1.2 |
12 |
|
5 |
1.2 |
2.0 |
5 |
|
|
|
ИТОГО |
51 |
Таким образом мы получили, что для оценки показателей механической торговой системы объем выборки (количество сделок на периоде тестирования) не должен быть меньше 51. Заметим, что при вычислении этого значения мы использовали минимально возможное число столбцов гистограммы (5 столбцов) и не очень широкий доверительный интервал (95%). С увеличением количества столбцов (уменьшением ширины столбца) и увеличением доверительного интервала минимально необходимый объем выборки может существенно вырасти.
13.5. Тестирование МТС.
Целью тестирования механической торговой системы является проверка ее работы на историческом ряде цен. Тестирование как правило проводят, используя пакеты технического анализа. По результатам тестирования программа формирует отчеты, на основании которых делаются выводы о качестве МТС.
При оптимизации системы, в правилах, описывающих открытие и закрытие позиций, постоянные параметры заменяются на оптимизируемые переменные (ОРТ-переменные), для которых задаются диапазон и шаг изменения. Затем программа проводит ряд тестов для всех возможных сочетаний ОРТ-переменных и формирует соответствующие отчеты. По результатам анализа этих отчетов выбирается такой набор параметров, при котором величина, разброс и устойчивость показателей системы являются оптимальными для трейдера.
Тестирование и оптимизацию системы рекомендуется проводить раздельно для длинных и коротких сделок.
Мы будем рассматривать следующие отчеты о тестировании системы: отчет о величине торгового счета (equity report), сгруппированный отчет о величине торгового счета, отчет о сделках (trades report), сводный отчет (results report).
ПРИМЕЧАНИЕ: далее в тексте содержание отчетов, а также обозначения показателей МТС и формулы для их вычисления могут отличаться от принятых в пакетах технического анализа.
13.6. Отчет о величине торгового счета.
Отчет о величине торгового счета показывает изменение стоимости портфеля на каждом ценовом баре. Отчет содержит следующие поля:
182
|
bar number |
Порядковый номер текущего временного периода (бара). |
|
date |
Дата/время текущего бара. |
|
position |
Торговая позиция на конец текущего бара. Возможны следующие типы позиций: "OUT" - вне рынка, "LONG" - длинная позиция, "SHORT" - короткая позиция. |
|
price |
Текущая цена актива. |
|
net change price |
Изменение цены актива за текущий период. |
|
% change price |
Процентное изменение цены актива за текущий период. |
|
equity |
Текущая величина торгового счета. |
|
net change equity |
Изменение величины торгового счета за текущий период. |
|
% change equity |
Процентное изменение величины торгового счета за текущий период. |
Сгруппированный отчет о величине торгового счета формируется на основе отчета о торговом счете и показывает изменение стоимости портфеля по укрупненным периодам времени. Отчет содержит следующие поля:
| ||||||
|
183 |
|
last date |
Последняя дата/время текущего периода. |
|
price |
Цена актива на конец текущего периода. |
|
net change price |
Изменение цены актива за текущий период. |
|
% change price |
Процентное изменение цены актива за текущий период. |
|
equity |
Величина торгового счета на конец текущего периода. |
|
net change equity |
Изменение величины торгового счета за текущий период. |
|
% change equity |
Процентное изменение величины торгового счета за текущий период. |
Отчет о сделках формируется на основе отчета о торговом счете и описывает каждую торговую операцию, сгенерированную системой. Приведем список полей отчета о сделках и некоторые формулы для вычисления показателей системы:
Общая информация о сделке
|
trade number |
Порядковый номер сгенерированной при тестировании сделки. |
|
trade type |
Тип сделки: "LONG" - длинная сделка, "SHORT" - короткая сделка. |
|
bars in trade |
Количество баров, в течение которых была открыта данная позиция. |
|
days in trade |
Число календарных дней, в течение которых была открыта данная позиция. |
|
max price in trade |
Максимальная цена актива от момента открытия позиции до момента ее закрытия. |
|
min price in trade |
Минимальная цена актива от момента открытия позиции до момента ее закрытия. |
|
|
184 |
|
Показатели, характеризующие вход в позицию enter bar Номер бара, на котором была открыта по- | ||||||||
|
|
enter efficiency Эффективность входа в позицию. Показатели, характеризующие выход из позиции exit bar Номер бара, на котором была закрыта по- | ||||||||
|
|
exit efficiency Эффективность выхода из позиции. Показатели, характеризующие сделку net profit Величина дохода по данной сделке (в день | ||||||||
|
закрытие позиции.
trade efficiency Эффективность сделки.
Эффективность входа в позицию показывает, насколько хорошо МТС в ходе конкретной сделки реализует потенциальную прибыль относительно цены входа в позицию и вычисляется по формулам:
- для длинных позиций
max price in trade - enter price
enter efficiency =-
max price in trade - min price in trade
- для коротких позиций
enter price - min price in trade
enter efficiency =-
max price in trade - min price in trade
Эффективность входа может принимать значения от 0 до 1.
Эффективность выхода из позиции показывает, насколько хорошо МТС в ходе конкретной сделки реализует потенциальную прибыль относительно цены выхода из позиции и вычисляется по формулам:
- для длинных позиций
exit price - min price in trade
exit efficiency =-
max price in trade - min price in trade
- для коротких позиций
max price in trade - exit price
exit efficiency =-
max price in trade - min price in trade
Эффективность выхода может принимать значения от 0 до 1.
Эффективность сделки показывает, насколько хорошо МТС в ходе конкретной сделки реализует общую потенциальную прибыль и вычисляется по формулам:
- для длинных позиций
exit price - enter price
trade efficiency =-
max price in trade - min price in trade
- для коротких позиций
enter price - exit price
trade efficiency =-
max price in trade - min price in trade
186
- общая формула
trade efficiency = enter efficiency + exit efficiency -1 Эффективность сделки может принимать значения от -1 до 1.
Считается что у МТС средняя эффективность входов и средняя эффективность выходов должна быть больше 0.6, то есть средняя эффективность сделки должна превышать 0.2. Анализ эффективностей наглядно показывает направления усовершенствования системы, так как позволяет раздельно оценить качество сигналов на вход в позицию и сигналов на выход из нее.
13.9. Сводный отчет.
Сводный отчет формируется на основе отчета о торговом счете и отчета о сделках и дает общую информацию о результатах тестирования системы. Приведем список полей сводного отчета и некоторые формулы для вычисления показателей системы:
Показатели, характеризующие линию торгового счета на периоде тестирования.
start date start equity
finish date finish equity
total bars
total days
net system drawdown % system drawdown
Дата начала тестирования.
Величина торгового счета на начало тестирования (начальные инвестиции).
Дата окончания тестирования.
Величина торгового счета после окончания тестирования.
Количество баров, в течение которых происходило тестирование.
Число календарных дней, в течение которых происходило тестирование.
Наибольшее снижение торгового счета относительно начальных инвестиций (в деньгах).
Наибольшее снижение торгового счета относительно начальных инвестиций (%).
187
Показатели, характеризующие доходность стратегии "купил и держи " на периоде тестирования.
|
buy&hold net profit Доход стратегии "купил и держи" на пе- | ||||
| ||||
|
формуле сложного процента). |
| ||||||
|
годовых по формуле сложного процента) Показатели, характеризующие сделки. total trades Общее число сделок. |
|
% in trade |
Доля времени на периоде тестирования, в течение которого система имела открытые позиции. |
|
% out trade |
Доля времени на периоде тестирования, в течение которого система была вне рынка. |
|
avg net profit |
Средний доход сделок (в деньгах). |
|
stdev net profit |
Среднеквадратичное отклонение дохода сделок (в деньгах). |
|
avg % profit |
Средний доход сделок (%). |
|
stdev % profit |
Среднеквадратичное отклонение дохода сделок (%). |
|
avg net drawdown |
Среднее наибольших снижений торгового счета (в деньгах). |
|
stdev net drawdown |
Среднеквадратичное отклонение наибольших снижений торгового счета (в деньгах). |
|
|
188 |
|
avg % drawdown |
Среднее наибольших снижений торгового счета (%). |
|
stdev % drawdown |
Среднеквадратичное отклонение наибольших снижений торгового счета (%). |
|
max net drawdown |
Наибольшее снижение торгового счета за отдельную сделку (в деньгах). |
|
max % drawdown |
Наибольшее снижение торгового счета за отдельную сделку (%). |
|
avg net win / |avg net loss| |
Отношение средней прибыли выигрышных сделок к среднему убытку проигрышных сделок. |
Показатели, характеризующие выигрышные сделки.
win trades Количество выигрышных сделок.
|
win trades % |
Процент выигрышных сделок. |
|
win amount |
Общая прибыль всех выигрышных сделок. |
|
avg net win |
Средняя прибыль выигрышных сделок (в деньгах). |
|
stdev net win |
Среднеквадратичное отклонение прибыли выигрышных сделок (в деньгах). |
|
max net win |
Максимальная прибыль выигрышной сделки (в деньгах). |
|
avg % win |
Средняя прибыль выигрышных сделок (%). |
|
stdev % win |
Среднеквадратичное отклонение прибыли выигрышных сделок (%). |
|
max % win |
Максимальная прибыль выигрышной сделки (%). |
|
avg bars win |
Средняя продолжительность выигрышных сделок (в барах). |
|
stdev bars win |
Среднеквадратичное отклонение продолжительности выигрышных сделок (в барах). |
|
|
189 |
| ||||
|
лок, следовавших одна за другой. Показатели, характеризующие проигрышные сделки. loss trades Количество проигрышных сделок. |
| ||||||||||||||||||||||||
|
сделок, следовавших одна за другой. Показатели, характеризующие эффективность сделок. avg enter efficiency Средняя эффективность открытия позиции. |
|
stdev enter efficiency |
Среднеквадратичное отклонение эффективности открытия позиции. |
|
|
190 |
avg exit efficiency stdev exit efficiency
avg trade efficiency stdev trade efficiency
Среднеквадратичное отклонение эффективности закрытия позиции.
Средняя эффективность сделок.
Среднеквадратичное отклонение эффективности сделок.
Приведем некоторые формулы для вычисления показателей механической торговой системы:
показатели доходности системы:
total trades
total net profit = ^ net profit (i)
i=1
total % profit = П(1 + % profit (i))-1
total % profit in year = (1 + total % profit)365/ totaI days - среднее значение и с. к. о. дохода сделок (в деньгах)
total trades
^ net profit (i)
avg net profit =
total trades
i =1
stdev net profit =
total trades
- ^ (net profit (i) - avg net profit )2
1 i=1
total trades -]
среднее значение и с. к. о. дохода сделок (в %)
1 /total trades
total trades
avg % profit = П(1+% profit (i))
V i=1
total trades
^ ln(1 + % profit (i))
-1
= exp
total trades
i=1
stdev % profit = (1 + avg % profit) x
„ (ln(1 + % profit (i)) - ^
1 i=1 V- ln(1 + avg % profit)
total trades /
total trades -
среднее значение и с.к.о. наибольших снижений торгового счета (в деньгах)
total trades
V net drawdown (i)
avg net drawdown =
total trades
i=1
stdev net drawdown =
total trades
I total trades -
- V {net drawdown (i) - avg net drawdown)
1 i=i
среднее значение и с. к. о. наибольших снижений торгового счета(в %)
¦, \1/total trades
i total trades \
avg % drawdown= П{і + % drawdown (i))
V i=i
1 total trades
= exp- V ln(1 + % drawdown (i))
_ total trades i=1
stdev % drawdown = (1 + avg % drawdown) x
total trades /
(ln(1 + % drawdown (i)) - ^2 total trades -1 ~~1 I - ln(1 + avg % drawdown)
Показатели МТС, характеризующие только прибыльные и только убыточные сделки, вычисляются аналогичным образом.
13.10. Математическое ожидание дохода сделки.
Важнейшим показателем, характеризующим качество МТС, является математическое ожидание дохода отдельной сделки. У прибыльной системы эта величина больше нуля. Задача состоит в том, чтобы по выборке сделок оценить математическое ожидание дохода и убедиться в том, что полученная оценка положительна и значимо отличается от нуля. Выборками случайных величин, на основе которых можно рассчитать выборочную среднюю и выборочное с.к.о. являются:
- в денежном выражении net profit,
- в процентах % profit.
Будем считать, что величина торгового счета не может упасть ниже нуля. Следовательно убыток по сделке не может быть меньше
192
торгового счета перед проведением сделки. С другой стороны, прибыль по сделке может быть неограничено большой. Значит плотность вероятности дохода и в денежном и в процентном выражении имеет положительную асимметрию. Для проверки гипотезы о величине математического ожидания дохода отдельной сделки правильнее будет перейти к случайной величине х = ln(1 + % profit) .
Пусть случайная величина х имеет математическое ожидание р и генеральную дисперсию О2. Оценками математического
ожидания и дисперсии по выборке (х1, х2,..., XN) будут выборочная средняя и выборочная дисперсия:
1 N _2 I N —
^ 7V (хк - X)2
'1 к=1
X = — V
ЛТ і—і
N-
к=1
где N = total trades.
При достаточно большом числе сделок доверительный интервал для р, характеризующийся доверительной вероятностью P,
задается в виде:
О
yfN
<р<X+t
1-q/2, v
1-q/2,v
где v = N -1, q = 1 - P.
Гипотеза о том, что оценка математического ожидания дохода отдельной сделки больше нуля формулируется в виде:
H0: X=0 H1 : X > 0
Проверка подобных гипотез подробно рассмотрена ранее в этой книге. Для более жесткой проверки гипотезы выборку (х1, х2xN ) усекают справа, то есть из нее исключают значения, превосходящие правую границу доверительного интервала, после чего пересчитывают величины X и О .
При изучении математического ожидания дохода отдельной сделки полезно рассмотреть вопрос о том, что определяет эту величину. Вернемся к формуле для вычисления среднего значения дохода сделок:
193 total trades
avg net profit = -
^ net profit (i)
total trades i=1
Эту формулу можно записать в другом виде, разделив сделки на прибыльные и убыточные: avg net profit =
win trades х avg net win - loss trades x | avg net loss |
total trades
Так как win trades
total trades loss trades total trades
= win trades %
= loss trades % = 1 - win trades % то
avg net profit = win trades % х avg net win -
- (1 - win trades %)x | avg net loss |
Из последней формулы следует, что система может быть прибыльной либо за счет увеличения процента прибыльных сделок, либо за счет увеличения отношения средней прибыли выигрышных сделок к среднему убытку проигрышных сделок. У прибыльной системы среднее значение дохода больше нуля, то есть отношение средней прибыли выигрышных сделок к среднему убытку проигрышных сделок соотносится с процентом выигрышных сделок следующим образом:
, .. | avg net loss |
win trades % >-
avg net win +1 avg net loss |
или
avg net win 1 - win trades %
| avg net loss | win trades %
Аналогичное соотношение для процентных показателей можно получить, используя формулу для вычисления среднего значения дохода сделок в %:
(1 + avg % profit)totaltrades =
= (1 + avg % win)win trades x (1 + avg % loss)loss trades
194
Из этого выражения следует, что
ln(1 + avg % profit) = win trades % x ln(1 + avg % win) -- (1 - win trades %)x | ln(1 + avg % loss) |
Для прибыльной системы выполняется условие
ln(1 + avg % win) 1 - win trades %
| ln(1 + avg % loss) | win trades %
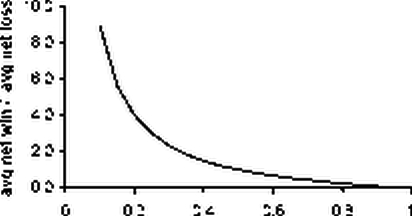
Связь между процентом выигрышных сделок и отношением средней прибыли выигрышных сделок к среднему убытку проигрышных сделок можно представить графически.
 |
|
win trades % |
Соотношение между процентом выигрышных сделок и отношением средней прибыли выигрышных сделок к среднему убытку проигрышных сделок можно ужесточить, используя показатели рассеяния:
/ stdev net win
--+
v | avg net loss |
avg net win x stdev net loss'' | avg net loss |2 y
avg net win | avg net loss |
- Sx
1 - win trades % >-
win trades %
195
где 5 - неотрицательное число, характеризующее запас прочности МТС - чем больше 5, тем выше запас прочности. У хороших систем последнее неравенство справедливо при 5 > 0.5 .
13.11. Кумулятивная кривая дохода сделок.
Кумулятивная кривая дохода сделок показывает изменение торгового счета от сделки к сделке. При оценке качества торговой системы полезно изучить эту кривую в полулогарифмическом масштабе. Для исключения влияния величины начальных инвестиций кривую можно нормировать. После этого полученная зависимость исследуется с применением регрессионного анализа. Зависимость величины торгового счета от номера сделки можно получить непосредственно из отчета о сделках.
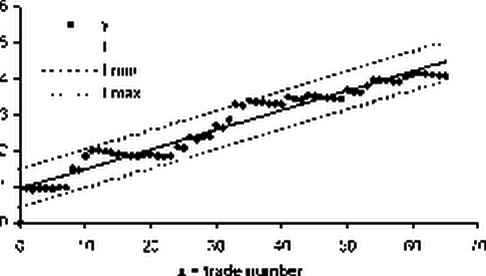
Рассмотрим результаты работы МТС, тестирование которой проводилось на временном ряде цен закрытия по индексу РТС в период с января 1996 г. по сентябрь 2002 г. За это время система совершила 65 сделок, то есть объем выборки равен 66: результаты после 65 сделок + результат до первой сделки (начальные инвестиции). На рисунке изображен логарифм эмпирической нормированной кумулятивной кривой дохода сделок (у), линейная аппроксимация (f) и 95%-ный доверительный интервал линии регрессии.
|
3 С О) Г го (Л 3 с О) II > |  |
196
ясненная дисперсия рассеяния эмпирических данных вокруг линии регрессии. Чем выше необъясненная дисперсия, тем больше разброс эмпирических точек, то есть выше риск системы. Отношение тангенса угла наклона линии регрессии к величине не-объясненного с.к.о. является сводным показателем, характеризующим и доходность и риск системы.
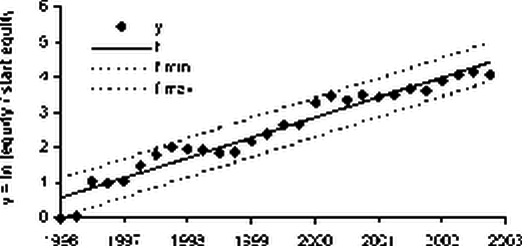
Кумулятивная кривая дохода сделок показывает изменение торгового счета от сделки к сделке. Для анализа поведения счета во времени используют сгруппированный отчет о величине торгового счета. Изучение поведения счета по укрупненным периодам времени полностью аналогично изучению кумулятивной кривой дохода сделок. Для той же механической системы на рисунке изображен логарифм эмпирической нормированной величины торгового счета на конец каждого квартала на периоде тестирования (у ), линейная аппроксимация (f) и 95%-ный доверительный интервал линии регрессии. Как правило, для анализа линии торгового счета выбираются месячные или квартальные данные.
 |
|
x = last date |
В этом параграфе будет показано, как на основании показателей МТС оценить вероятность получения убытка в серии последовательных сделок.
Для упрощенного расчета вероятности убытка используем три показателя МТС, которые приведены в сводном отчете:
197
win trades % - процент прибыльных сделок системы, avg %win - средняя величина выигрыша (%), avg %loss - средняя величина проигрыша (%).
Введем обозначения:
N - заданная длина серии сделок, n - количество выигрышных сделок в серии,
(N — n) - количество проигрышных сделок в серии, p - вероятность выигрыша (p = win trades %), total % profit - доход по итогам серии сделок.
Будем приближенно считать, что все выигрышные сделки будут приносить одинаковый доход avg %win, а все проигрышные сделки будут приносить одинаковый убыток avg %loss . Тогда, если задано количество сделок и вероятность выигрыша, то доход является функцией от числа выигрышных сделок и равен
total % profit (п) = (1 + avg %win)n х (1— | avg %loss |)N—n - 1
Вероятность появления в серии определенного числа выигрышных сделок описывается биномиальным распределением:
N! N
Prob(n) = -- pn (1 - p) — n n = 0,1,...,N
n! (N-n)!
Количество всех возможных комбинаций числа выигрышных и числа проигрышных сделок в серии длиной N будет равно N +1. Для всех этих комбинаций необходимо рассчитать величину дохода total % profit (n) и соответствующую ей вероятность Prob(n) . Тогда вероятность убытка можно найти как:
N
Prob loss = ^ Prob(n)
n=0
где соответствующее слагаемое входит в сумму при условии, что total % profit (n) < 0.
Приведем пример такого расчета для торговой системы при длине серии последовательных сделок равной N = 20. Пусть величина показателей системы составляет
198
p = win trades % = 45%
avg %win = 8% avg %loss = -5%
Эта система имеет положительное математическое ожидание дохода в расчете на одну сделку
avg % profit = (1 + avg %win)p x (1- | avg %loss |)1-p -1 avg % profit = 0.64%
В приведенной ниже таблице содержатся все возможные комбинации числа выигрышных и числа проигрышных сделок, а также соответствующие этим комбинациям величины дохода по итогам серии сделок и вероятности.
|
n |
(N - n) |
total % profit |
Prob |
Prob loss |
|
0 |
20 |
-64.15% |
0.0006% |
0.0006% |
|
1 |
19 |
-59.25% |
0.0105% |
0.0105% |
|
2 |
18 |
-53.67% |
0.0816% |
0.0816% |
|
3 |
17 |
-47.33% |
0.4006% |
0.4006% |
|
4 |
16 |
-40.12% |
1.3930% |
1.3930% |
|
5 |
15 |
-31.93% |
3.6471% |
3.6471% |
|
6 |
14 |
-22.61% |
7.4600% |
7.4600% |
|
7 |
13 |
-12.02% |
12.2072% |
12.2072% |
|
8 |
12 |
0.02% |
16.2300% |
|
|
9 |
11 |
13.70% |
17.7055% |
|
|
10 |
10 |
29.26% |
15.9349% |
|
|
11 |
9 |
46.95% |
11.8524% |
|
|
12 |
8 |
67.06% |
7.2731% |
|
|
13 |
7 |
89.92% |
3.6620% |
|
|
14 |
6 |
115.91% |
1.4981% |
|
|
15 |
5 |
145.46% |
0.4903% |
|
|
16 |
4 |
179.05% |
0.1254% |
|
|
17 |
3 |
217.23% |
0.0241% |
|
|
18 |
2 |
260.64% |
0.0033% |
|
|
19 |
1 |
309.99% |
0.0003% |
|
|
20 |
0 |
366.10% |
0.00001% |
|
|
|
|
ИТОГО |
100% |
25% |
199
В данном случае система с положительным математическим ожиданием дохода после достаточно длинной серии сделок с вероятностью 25% принесет убыток. Можно привести другие примеры, где МТС с отрицательным математическим ожиданием после серии сделок с достаточно высокой вероятностью приносит прибыль. То есть при биржевой торговле в силу естественных законов статистики правильные решения не всегда сопровождаются прибылью, а неправильные - убытком.
Следует помнить, что приведенная выше оценка вероятности убытка после серии сделок строилась на том, что все выигрышные сделки приносят одинаковый доход avg %win, а все проигрышные сделки приносят одинаковый убыток avg %loss . Это является достаточно грубым приближением, которое не учитывает разброс результатов конкретной сделки. Более точная оценка вероятности убытка основана на многократном численном моделировании результатов серии сделок по методу Монте-Карло. Принципиальная схема такого алгоритма имеет вид:
1) Задание входных данных
1.1) Из отчета о сделках массив значений доходов сделок {% profit (к )}
к = 1,...,total trades
1.2) Количество розыгрышей M (чем больше розыгрышей, тем достовернее результат).
1.3) Длина серии сделок N .
2) Вычисление вспомогательного массива {х(к)} х(к) = ln(1 + % profit (к))
к = 1,...,total trades
3) Вычисление в табличном виде гистограммы плотности вероятности значений величины х (методика подробно изложена в главе 6).
4) Вычисление в табличном виде интегральной функции распределения значений величины х на основании полученной в предыдущем пункте гистограммы.
5) Задаем стартовое значение номера текущего розыгрыша m = 0.
200
6) Задаем стартовые значения количества розыгрышей, приводящих к убытку N loss = 0
7) Номер текущего розыгрыша m = m +1
8) Проводим отдельный розыгрыш результатов сделок:
8.1) Генерируем набор случайных чисел в количестве N, равномерно распределенных в интервале от 0 до 1.
8.2) Из равномерно распределенного набора случайных чисел с помощью полученной на шаге 4 интегральной функции получаем набор случайных чисел, распределенных как величина x . Обозначим этот набор как {y(i)}, i = 1,..., N.
8.3) Находим сумму массива случайных чисел у
N
S = Z y(i)
i=1
8.4) Находим текущее значение количества розыгрышей, приводящих к убытку:
если S < 0, то N loss = N loss +1
9) Если номер текущего розыгрыша m меньше, чем общее число розыгрышей M , то переходим на шаг 7.
10) После того, как сделаны все розыгрыши (то есть m = M), вычисляем вероятность убытка
Probloss = ^
M
13.13. Вероятность разорения в серии последовательных сделок.
Вероятность разорения - это вероятность того, что в серии последовательных сделок по сигналам МТС величина убытков в силу естественных законов статистики превысит заранее заданное критическое значение. Это может привести к остановке торговли и ошибочному отказу от на самом деле прибыльной МТС.
Аналитический расчет вероятности разорения связан со значительными трудностями ввиду того, что получение критического убытка зависит не только от показателей системы (процента прибыльных сделок, средней величины выигрыша, средней величины проигрыша), но и от очередности прибыльных и убыточных сделок. В результате неблагоприятной последова
201
тельности сделок при работе с прибыльной системой разорение может наступить раньше, чем система докажет свое статистическое преимущество.
Так как критический убыток может быть получен до окончания серии сделок, то аналитический расчет вероятности разорения приводит к необходимости учета не только всех возможных сочетаний числа прибыльных и числа убыточных сделок в серии, но и анализу для каждого такого сочетания всех возможных последовательностей сделок. Это весьма трудоемкая задача, особенно для длинных серий.
В данном случае вычисление вероятности разорения гораздо проще можно провести численно путем многократного моделирования результатов серии сделок по методу Монте-Карло. Изложим принципиальную схему алгоритма:
1) Задание входных данных
1.1) Из отчета о сделках массив значений доходов сделок {% profit (k )}
k = 1,...,total trades
1.2) Количество розыгрышей M (чем больше розыгрышей, тем достовернее результат).
1.3) Длина серии сделок N .
1.4) Критическое значение убытка % max loss .
2) Вычисление вспомогательного массива {x(k)} x(k) = ln(1 + % profit (k))
k = 1,...,total trades
3) Вычисление в табличном виде гистограммы плотности вероятности значений величины x (методика подробно изложена в главе 6).
4) Вычисление в табличном виде интегральной функции распределения значений величины x на основании полученной в предыдущем пункте гистограммы.
5) Задаем стартовое значение номера текущего розыгрыша m = 0.
6) Задаем стартовые значения количества розыгрышей, приводящих к разорению N max loss = 0
7) Номер текущего розыгрыша m = m +1
202
8) Проводим отдельный розыгрыш результатов сделок:
8.1) Генерируем набор случайных чисел в количестве N, равномерно распределенных в интервале от 0 до 1.
8.2) Из равномерно распределенного набора случайных чисел с помощью полученной на шаге 4 интегральной функции получаем набор случайных чисел, распределенных как величина x . Обозначим этот набор как {у(і)}, і = 1,..., N.
8.3) Задаем стартовое значение суммы (нарастающим итогом) массива случайных чисел y : S = 0
8.4) Задаем стартовое значение номера случайного числа из массива y : і = 0
8.5) Номер текущего случайного числа из массива у : і = і +1
8.6) Находим текущее значение суммы массива случайных чисел у : S = S + у(і)
8.7) Проверяем, наступило ли разорение: если S < ln(1- | % max loss |)
то разорение достигнуто, поэтому находим текущее значение количества розыгрышей, приводящих к разорению N max loss = N max loss +1 и переходим на шаг 7.
8.8) Если номер текущего случайного числа і меньше, чем длина серии N, то переходим на шаг 8.5. В противном случае переходим на шаг 9.
9) Если номер текущего розыгрыша m меньше, чем общее число
розыгрышей M , то переходим на шаг 7.
10) После того, как сделаны все розыгрыши (то есть m = M), вычисляем вероятность разорения
N max loss
Prob max loss =-
M
