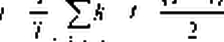Сглаживание динамических рядов

11.1. Введение.

Целью сглаживания динамического ряда является фильтрация случайных колебаний уровней этого ряда и выявление наиболее устойчивой тенденции движения. Мы будем рассматривать методы сглаживания, базирующиеся на вычислении скользящих средних. Любое скользящее среднее - это метод определения среднего уровня динамического ряда за некоторый период времени. Термин "скользящее" подразумевает, что среднее значение каждый раз заново вычисляется в последовательные моменты времени. В этой главе под динамическим рядом мы, как правило, будем понимать ряд, состоящий из цен активов.

11.2. Типы скользящих средних.

В общем виде формула для вычисления любой скользящей средней (moving average) имеет вид:

^MA = Z ™кУк

к

где {у_к } - массив цен актива,

{w_k } - массив весов, с которыми цены входят в формулу.

При этом для набора весов должно соблюдаться правило нормирования:

Z ^wk =¹

к

Скользящая средняя характеризуется:

- объектом вычисления, то есть тем динамическим рядом, который необходимо сгладить,

- периодом скользящей средней,

- типом скользящей средней, который определяет алгоритм вычисления набора весов {w_k } .

Различают три основных типа скользящих средних:

- простая скользящая средняя (SMA - simple moving average),

- взвешенная скользящая средняя (WMA - weighted moving average),

- экспоненциальная скользящая средняя (EMA - exponential moving average).



11.3. Простая скользящая средняя.

Простая скользящая средняя порядка T - это средняя арифметическая цен за период времени [t — T +1, t], то есть


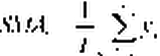
Внутри интервала t — T +1 < k < t все веса, с которыми входят цены при расчете скользящей средней одинаковы и равны w_k = 11T. За пределами этого интервала, то есть при k < t — T +1 веса равны нулю.

Первым недостатком SMA является равенство весов в пределах интервала расчета, так как интуитивно понятно, что последние данные должны иметь большую ценность, то есть входить в формулу для расчета с большим весом.

Второй недостаток SMA становится понятным при рассмотрении рекуррентной формулы для ее вычисления:

¹У

T^yt—t

SMA, = SMA,—1 + T У,

Очевидно, что SMA на каждую цену реагирует дважды: первый раз, когда цена входит в интервал расчета, и второй раз, когда цена выбывает из него. Вторая реакция никак не связана с текущей динамикой и, следовательно, нежелательна.

Традиционно, скользящую среднюю соотносят с последней точкой интервала расчета, то есть с моментом времени t , хотя, строго говоря, это некорректно. Вычисленное значение SMA нужно ставить в соответствие с точкой на оси времени, имеющей координату

(T — 1) 1

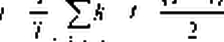
то есть с точкой, сдвинутой влево по оси времени от момента t на величину At = (T — 1) / 2 .

11.4. Взвешенная скользящая средняя.

Взвешенная скользящая средняя придает больший вес последним данным. Она рассчитывается путем умножения каждой

156

цены в пределах периода времени [t - T +1, t] на соответствующий вес. В простейшем случае при линейно убывающих весах от момента t до момента t — T +1 формула имеет вид:

2 ^t

wma, = ттт-г В*—(t—T)]-y,

^{T (T} + 4 k=t—T+1

Цена в момент времени k = t входит в формулу для расчета с максимальным весом w = 2 /(T +1), а цена в момент времени

k = t — T +1 входит в формулу для расчета с минимальным весом w = 2 /(T • (T +1)) .

При отсутствии специализированных программ технического анализа, для расчета линейно взвешенной скользящей средней может быть полезна рекуррентная формула

2

T+1)

WMA,—,+ T у,

2

T (T +1) ^у—T

WMA_t

SMA_t

Из этой формулы следует, что реакция WMA на выбытие цены из интервала расчета менее выражена, чем у SMA, и эта реакция тем меньше, чем больше период скользящей средней.

11.5. Экспоненциальная скользящая средняя.

Как и в случае взвешенной средней, экспоненциальная скользящая средняя придает больший вес последним данным, однако при расчете используется вся история цен. Рекуррентная формула для ее вычисления имеет вид:

EMA_t = a • y_t + (1 — a) • EMA_t—1 0 < a < 1

Показательный процент a определяет степень сглаживания. Чем больше a , тем меньше степень сглаживания. При a = 1 экспоненциальная скользящая средняя равна цене.

EMA лишена недостатка, присущего SMA и WMA, связанного с фиксированным интервалом расчета скользящей средней.

Формулу для вычисления EMA можно записать в явном виде, если предположить, что в нулевой момент времени скользящая средняя совпадает с ценой ( EMA₀ = у₀ ):

157

EMA_t = a ¦ y_t + (1 -a) ¦ EMA_t __A =

= a-y_t +a-(1 -a)¦ y_t-1 + (1 -a)² ¦ EMA_t-2 =

= a^y_t + a-(1 -a)¦ y_t-1 + a-(1 -a)² ¦ y_t-2 + (1 -a)³ ¦ EMA_t3 =

= a-yt + a^(1 -a>y_t__x + a^(1 -a)² ¦ y_t-2 + к + (1 -a) ¦ y₀ Следовательно

^EMAt = ^aI ^{(1 - a)} ’ ¦ yt-. + ^{(1 - a)}‘ ¦ Уо

i=0

или (эквивалентная форма записи)

^EMAt = ^aI^{(1 -a)}‘^-k ¦Ук + ^{(1 -a)}‘ ¦Уо

к=1

Вычисленное значение EMA нужно ставить в соответствие с точкой на оси времени, имеющей координату

t = aI (1 - a). (t - i) = taI (1 - a)ⁱ - aI (1 - a) i

i=0

1=0

i =0

Суммы в последней формуле вычисляются как

1 - (1 -a)^t

I (1 -a =

i=0

I^{(1 -a)i} ¦. =

(1 -a) - (1 + at - a)(1 - a)^t

i=0 ^a

После несложных преобразований получаем, что

=t - +o-ai

При достаточно большом t, т.к. (1 -a) < 1, то ^{(1 -a) t}+¹ « ^ значит можно пренебречь последним слагаемым и написать приближенное выражение t « t - (1 - a)/ a.

Период ЕМА

Момент времени t сдвинут влево по оси времени от момента t на величину At = (1 -a)/a. Если по аналогии с простой скользящей средней обозначить эту величину как

158

At = (T - 1) / 2 , где T является периодом, то связь периода и показательного процента задается выражением:

(1 -а) = (T -1)

а 2

Отсюда следуют формулы для конвертирования показательного процента в период и наоборот:

С учетом этих соотношений можно переписать рекуррентную формулу для ЕМА:

EMA_t

• EMAt-1

2 T -1

--y_t +--

T +1 ^t T +1

ЕМА произвольного порядка

До сих пор мы рассматривали экспоненциальную скользящую среднюю первого порядка, то есть сглаживанию подвергался непосредственно исходный динамический ряд:

EMA- = а • y_t + (1 -а) • EMA-

При обозначении ЕМА первого порядка верхний индекс обычно опускается.

Экспоненциальная скользящая средняя произвольного n -го порядка задается формулой:

EMA\ⁿ⁾ = а • EMA(^n-l) + (1 -а) • EMA-

DEMA

Рассмотрим ошибку ЕМА, то есть величину e_t = y_t - EMA_t.

Если прибавить к значению экспоненциальной скользящей средней цены значение экспоненциальной скользящей средней ошибки, то такая величина называется двойной экспоненциальной скользящей средней:

DEMA_t = EMA_t + EMA(e_t) = EMA_t + EMA(y_t - EMA_t) =

= 2 • EMA_t - EMA(EMA_t) = 2 • EMA- - EMA(²⁾

159

TEMA

Рассмотрим ошибку DEMA, то есть величину e_t = y_t — DEMA_t. Тогда тройная экспоненциальная скользящая средняя вычисляется по формуле:

TEMA_t = DEMA_t + EMA(e_t) = DEMA_t + EMA(y_t — DEMA_t)

После преобразований получим, что

TEMA_t = 3 • EMA_t — 3 • EMA(EMA_t) + EMA(EMA(EMA_t)) =

= 3 • EMA^ — 3 • EMA_t⁽²⁾ + EMAf⁾

11.6. Точки пересечения экспоненциально сглаженных кривых.

Часто в момент времени t ("сегодня") необходимо знать, какая цена должна быть в момент времени t +1 ("завтра"), чтобы произошло пересечение цены у с какой-либо экспоненциально сглаженной кривой или пересечение двух различных экспоненциально сглаженных кривых. Приведем соответствующие формулы для некоторых наиболее важных случаев.

1) Пересечение цены y и ЕМА 1-го порядка

у,+1 = ema;¦>

2) Пересечение цены y и ЕМА 2-го порядка

EMA(²⁾ +a^EMA(^V)

у,+і =-—-—

1 + a

3) Пересечение цены у и DЕМА

= (1 - а) • ((2 - а) • EMA⁽1 - EMAⁱt¹⁾) ^+¹ 1 — а • (2 — а)

или

у,+1 =-

(1 — а) • (PEMA_t — a • EMA^<t^r>)

1 — а- (2 — а)

4) Пересечение двух ЕМА 1-го порядка различных периодов

_у = (1 — а₂) • EMA2⁽1 — (1 — а) • EMA1⁽P

^у,+1 =

12

160

EMA1⁽¹⁾ характеризуется показательным процентом а₁, EMA2⁽¹⁾ характеризуется показательным процентом а₂.

5) Пересечение двух ЕМА 2-го порядка различных периодов

y_t+1 = [а₂ • (1 -а₂)• EMA2⁽(⁾ + (1 -а₂)• EMA2(²⁾ --а₁ • (1 -а₁)• EMAlf -(1 -а₁)• EMA1⁽⁽²⁾]/[а² -а₂²]

EMA1⁽¹⁾ и EMA1⁽²⁾ характеризуются показательным процентом а,

EMA2⁽¹⁾ и EMA2⁽²⁾ характеризуются показательным процентом а₂ .

6) Пересечение ЕМА 1-го порядка (показательный процент а₁) и ЕМА 2-го порядка (показательный процент а₂)

у₊₁ = [а₂ • (1 -а₂)• EMA2⁽⁽¹⁾ + (1 -а₂)• EMA2(²⁾ -

-(1 -а)• EMA^y^ -а₂²]

11.7. Выбор величины показательного процента для экспоненциальной скользящей средней.

Для того, чтобы оценить, насколько хорошо подобрана величина показательного процента а, необходимо рассмотреть ошибки, возникающие при прогнозировании уровня цены в момент времени t +1 ("завтра") значением ЕМА в момент времени t ("сегодня"). Введем обозначения:

- y_t - цена в момент времени t ,

- а - показательный процент сглаживания ряда цен,

- Y_t - ЕМА для ряда цен, т.е. Y_t = а • y_t + (1 -а) • Y_t-1,

- f_t - прогноз цены, причем f_t+1 = Y_t,

- e_t - ошибка прогноза, т.е. e_t = y_t - f_t,

- в - показательный процент сглаживания ряда квадратов ошибок прогноза,

- Q_t - ЕМА для ряда квадратов ошибок прогноза, т.е.

Qt =?• et² + (1 -#)• Q_t-1.

161

Оптимизация величины показательного процента a - это подбор такого его значения, чтобы при фиксированном в добиться того, чтобы Q_t ^ min . Обычно величину в выбирают в пределах от 0.1 до 0.2, что приблизительно соответствует периоду сглаживания в пределах от 10 до 20.

11.8. Экспоненциальная скользящая средняя с переменным показательным процентом.

На нестабильных рынках имеет смысл использовать ЕМА с переменным показательным процентом, который по мере получения новых данных постоянно подстраивается к текущей рыночной ситуации. Введем обозначения:

- y_t - цена в момент времени t,

- a_t - переменный показательный процент сглаживания ряда цен,

- Y_t - ЕМА для ряда цен, т.е. Y_t =a_t • y_t + (1 -a_t) • Y_t1,

- f_t - прогноз цены, причем f_t+1 = Y_t,

- e_t - ошибка прогноза: e_t = y_t - f_t,

- в - показательный процент сглаживания ошибок прогноза и модулей ошибок прогноза,

- E_t - ЕМА ошибок прогноза: E_t = в • e_t + (1 - в) • E_t-1,

- A_t - ЕМА модулей ошибок : A_t = в^ф | e_t | +(1 - в) • A_t-1. Значение переменного показательного процента в каждый момент времени вычисляют по формуле a_t =| E_t / A_t |. Величину в выбирают в пределах от 0.1 до 0.2.

11.9. Дисперсия скользящих средних.

Рассмотрим на качественном уровне вопрос о том, как соотносится дисперсия значений исходного динамического ряда с дисперсией скользящей средней этого ряда. Для простоты будем предполагать, что исходный динамический ряд состоит из слу-

2

чайных величин, имеющих одинаковую дисперсию G , причем в пределах интервала сглаживания средняя величина коэффици

162

ента корреляции между значениями исходного ряда в различные моменты времени равна р .

В общем виде формула для вычисления любой скользящей средней имеет вид:

^Y = Z ^wkyk

k

Дисперсия случайной величины, являющейся линейной комбинацией коррелированных случайных величин равна:

Z ^w2ol + ²ZZ ^Wi^Wk РгОг^Ок

О_У

k k i>k

Используя допущения о постоянстве дисперсий и коэффициентов корреляций, эту формулу можно упростить:

° = ^О Z ^wk + ¹р°² ZZ

'V² = ^О Z k

k

Следовательно

2

О

^WWk

k i>k

2 =Z w2 + 2pZZ^

^o k

k i >k

Согласно правилу нормирования весов справедливо равенство

^wi^wk

Z W + 2ZZ

i>k

Отсюда можно сделать вывод, что так как р < 1, то oY < О².

Дисперсия простой скользящей средней

Формула для простой скользящей средней имеет вид:

1 ^f

Y = _T Z Xk

^T k=t-T+1

Найдем суммы весов, входящие формулу для вычисления отношения дисперсии скользящей средней к дисперсии исходного ряда:



Z W = Z (1/t )² = -





2 Z Zww = 2 Z Z(1/T)² = _T



163

_2

В итоге получаем: —— = —+ р ¦

о² T T

Дисперсия экспоненциальной скользящей средней

Формула для экспоненциальной скользящей средней имеет вид:

Y = ^а?⁽¹ - а)' ¦ y_t__t +⁽¹ - а) ² ¦ Уо

i=0

Приведем выражения для сумм весов, входящие в формулу для вычисления отношения дисперсии скользящей средней к дисперсии исходного ряда:

? W = (1 -а)²² +а² ? (1 -а)^2к =¦

к=0 k=1

²² 2 - 2а 2 - 2а ^ _ч22

¦(1 -а)^2і

.2/1 __\22 . 2^/і __ч 2к ^а , ^{2 2а} /і __ч 22

¦ + ¦

2 -а 2 -а

(1 -а)²

2??

к=0i=k+1

При достаточно большом t, так как (1 - а) < 1, то <sup>(1 -а)2

W</sup>Wk =¦

2 -а 2 -а

0.

Следовательно

о2 а 2 - 2а 1 T -1

+ Р--= ~ + Р-

о² 2 -а

2 -а T



Содержание раздела

---