Применение МНК при изучении динамических рядов
10.1. Введение.
Аналитическая аппроксимация динамического временного ряда, содержащего цены некоторого актива в последовательные моменты времени, представляет собой математическую модель развития во времени этого динамического ряда и описывает присущие ему статистические характеристики.
Аналитическая аппроксимация содержит в себе некоторую условность, связанную с тем, что цена актива рассматривается как функция времени. На самом деле цена зависит не от того, сколько времени прошло с начального момента, а от того, какие факторы на нее влияли, в каком направлении и с какой интенсивностью они действовали. Зависимость от времени можно рассматривать как внешнее выражение суммарного воздействия этих факторов. Удовлетворительным образом аппроксимировать динамический ряд с помощью метода наименьших квадратов возможно лишь тогда, когда воздействие всех влияющих факторов однородно на всем рассматриваемом промежутке времени.
В случае, если динамический ряд цены актива удается аппроксимировать аналитической функцией времени с соблюдением допущений МНК, становится возможной экстраполяция этой функции, то есть прогноз цены в будущие моменты времени. Однако при этом стоит помнить, что при прогнозе неявным образом предполагается, что те же самые условия, в которых формировались цены в прошлом, будут существовать и в будущем. Использование экстраполяции в изменившихся условиях будет приводить к ошибкам, выходящим за рамки обычных для МНК погрешностей, связанных с шириной полосы неопределенности линии регрессии. Долгосрочные прогнозы сопряжены с большими ошибками, чем краткосрочные. Во-первых, это связано с расширением полосы неопределенность линии регрессии при удалении от центра тяжести эмпирических данных, по которым эта линия была получена. Во-вторых, это связано с возрастанием влияния новых факторов при увеличении периода прогноза.
Для того, чтобы динамический ряд можно было эффективным образом аппроксимировать с применением МНК, этот ряд должен удовлетворять следующим условиям:
- быть достаточно длинным,
- быть как можно менее волатильным.
При этом следует сказать, что применение МНК при изучении временных рядов имеет следующие особенности:
- для адаптирования регрессионной модели к изменяющимся условиям необходимо периодически пересчитывать параметры модели с учетом новых данных, а иногда возможно пересматривать саму модель,
- при расчете параметров регрессии все эмпирические данные входят с одинаковым весом, хотя интуитивно понятно, что более поздние данные имеют большую ценность.
10.2. Модель динамики цен активов.
Биржевые цены активов формируются как результат совместных действий большого количества участников рынка и, как следствие этого, в них присутствует случайная составляющая.
Рассмотрим временной ряд, состоящий из последовательных значений цены некоторого актива P1,P2,...,Pt. Цена не может быть отрицательной, но может принимать сколь угодно большие положительные значения. Следовательно, и отношение цен в последовательные моменты времени Pk / Pk_ также не
может оказаться ниже нуля, но может быть сколь угодно большим. Значит плотность вероятности цен активов и плотность вероятности отношения цен должны иметь положительную асимметрию.
Ситуация меняется при переходе к логарифмам отношения цен, то есть к величине Ayk = ln(Pk / Pk_ ) . Распределение логарифмов уже может быть симметрично и возможна его аппроксимация одним из аналитических законов распределения, которые были рассмотрены во второй главе (как правило обобщенным экспоненциальным распределением). При этом логарифм цены в произвольный момент времени складывается из логарифма цены в начальный момент времени (эта величина пред
139
полагается нестохастической) и суммы логарифмов отношения цен:
ln(P) = ln(P0) + ? ln«- / P„-t)
k=1
Если величины Ayk = ln(Pk / Pk_1) независимы и имеют конечную дисперсию, то согласно центральной предельной теореме величина y, = ln(P,) будет нормально распределена при любом
законе распределения Ayk . Так как логарифм цены распределен
нормально, то цена подчиняется логнормальному распределению.
Итак, если все случайные величины Ayk независимы и подчиняются одному и тому же закону распределения с математи-
„2
ческим ожиданием и и дисперсией о , то случайная величина ln(Pt) будет иметь нормальное распределение с математическим ожиданием и, и дисперсией о2,. Следовательно, логарифм цены в произвольный момент времени можно записать как ln(Pt) = ln(P0) + и, + o4t z
где случайная величина z подчиняется стандартному нормальному распределению.
Рисковые активы имеют положительное математическое ожидание дохода, следовательно и > 0 . Величина и определяет тренд актива, то есть воздействие на цену постоянно действующих систематических факторов.
Величина о определяет волатильность актива, то есть воздействие на цену множества случайных факторов.
Отношение ожидаемого дохода к ожидаемому риску за единицу времени и /о характеризует степень устойчивости роста цены актива. Чем выше это отношение, тем привлекательнее при прочих равных условиях инвестиции в данный актив.
Наряду с влиянием постоянно действующих факторов и случайных колебаний, цена актива может испытывать воздействие причин, характеризующихся циклическими колебаниями. Возникновение циклов связано с изменением оценки инвесто
140
рами ожидаемого дохода актива. С учетом периодических компонент модель динамики цены можно представить в виде
M
1n(Pt) = 1п(р0) + ^t + 2Rm cos(2nt/Tm +?т) + &4t Z
m=1
где Tm - период колебания, Rm - амплитуда колебания, ?т - начальная фаза. Существует эмпирическое правило, которое называют принципом пропорциональности, согласно которому амплитуды колебаний прямо пропорциональны их периодам. Для выделения отдельных гармоник из временного ряда цены актива используют анализ Фурье.
С учетом вышесказанного, исследование динамики цены актива должно включать в себя следующие этапы:
- определение тренда,
- определение циклических компонент,
- составление прогноза цены актива.
10.3. Определение тренда.
В качестве исходных данных рассмотрим цены закрытия по индексу Доу Джонса на последний торговый день месяца за период с 1932 по 1999 год.
|
Индекс Доу Джонса |
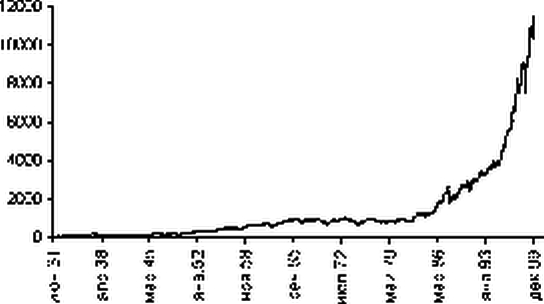 |
141
|
Индекс Доу Джонса |
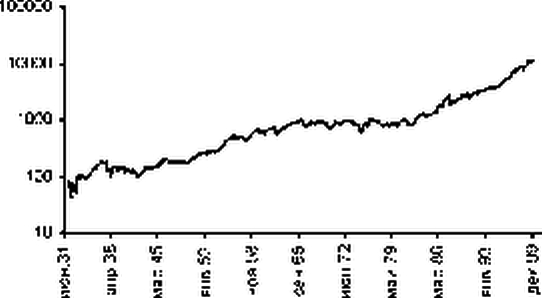 |
Для построения регрессионной модели в качестве фактора (независимой переменной) будем использовать номер месяца. При этом первый месяц в выборке (январь 1932 года) получает номер 0, последний месяц в выборке (декабрь 1999 года) получает номер 815, то есть tk = 0,...,815 . Объем выборки N = 816 точек.
Откликом (зависимой переменной) является логарифм цены закрытия yk = ln(Pk ). Эмпирическая зависимость отклика от фактора приведена на рисунке:
|
Эмпирическая зависимость |
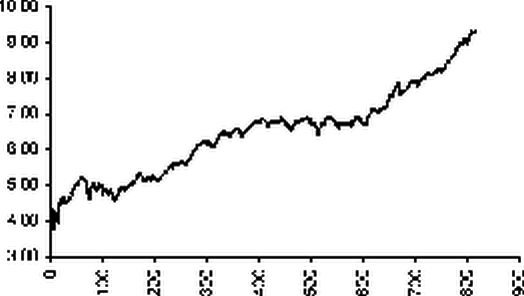 |
|
142 |
Примем гипотезу о том, что связь фактора и отклика выражается линейной функцией f (t) = at + b . Оценки параметров линейной регрессии проводятся по формулам:
N
Z!tyt -N-T¦ Y
k=1_
a=
N -2
Z tk - N ¦ T
k=1
где
- 1 N Y=N Z yk
- 1 N t=— Z tk
Nk
k=1
k=1
Вычисленные значения параметров составляют: a = 0.005, b = 4.402
Эмпирическая зависимость и линейная аппроксимация изображены на рисунке:
|
Эмпирическая зависимость и линейная аппроксимация |
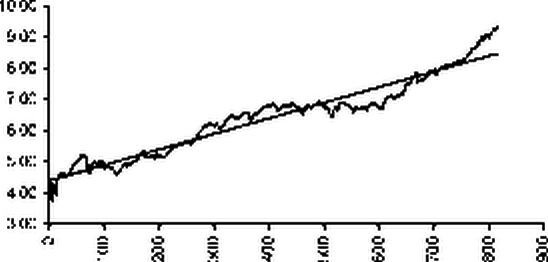 |
имеет вид:
143
Дисперсия оценок параметров линейной регрессии
Оценка дисперсии случайных отклонений отклика Y от линии регрессии (необъясненная дисперсия) вычисляется по формуле:
(Ук - atk - Ъ)
1 N 1
|
Ошибки линейной аппроксимации |
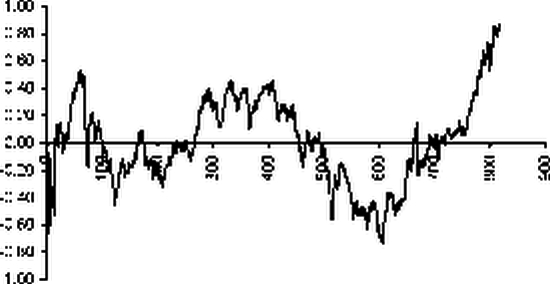 |
Вычисленные значения необъясненной дисперсии и соответствующее с.к.о. равны:
1 Ъ e2 = 1
а2 = 0.098
а„ = 0.313
Оценка дисперсии параметров а и Ъ выражаются формулами:
ъ
к=1
а2 =_а
^ а N
_2 _ аЪ = N
Ъ (Х - X)2 N
к=1
к=1
Расчетные значения этих величин по выборке составляют:
а2 = 2.2 • 10-9 аа = 4.7 -10-5
а2 = 4.8 • 10-4
аЪ = 2.2 -10-
Коэффициент детерминации
Качество линии регрессии характеризуется коэффициентом детерминации:
144
Z е,2
k=1
Z (У, - Y)2
k=1
В рассматриваемом случае эта величина равна R2 = 0.9348. Так как среднеквадратичные отклонения отклика Y и ошибок аппроксимации е связаны соотношением ое = ? 1 - R2 •о y, то получаем, что с.к.о. ошибок приблизительно в четыре раза меньше с.к.о. отклика: ое = 0.255оу.
е у
10.4. Статистические выводы о величине параметров регрессии.
Необходимо убедиться, что значения параметров регрессии значимо отличаются от нуля. Для проверки этого выдвигаются гипотезы:
H 0 : a = 0 H 0 : b = 0
H1 : a 0 H1 : b ^ 0
1) Примем величину уровня значимости q = 0.05
= 106.4
ta =
2) Рассчитаем критерии проверки a 0.005
о „ 4.7 -10-
4.402
= 200
tb =
оъ 2.2-10"
3)
4)
Правило принятия решения
Принять Н0 , если - t1-q / 2, V ^ t ^ t1-q/2,?
В противном случае принять Н1 , то есть Н1 принимается, когда критерий проверки t попадает в критическую область
I t I > t1-q/2, V
Расчет границ критической области
145
t1-q/2,? = СТЬЮДРАСПОБР(д, N - 2) =
= СТЬЮДРАСПОБР(0.05, 814) = 1.96
5) Проверка гипотезы
Так как критерии проверки для обоих параметров регрессии находятся в критической области, мы принимаем гипотезу Н1. Это означает, что при заданном уровне значимости параметры регрессии статистически значимо отличаются от нуля.
Статистические выводы о величине коэффициента детерминации
Убедимся в том, что коэффициент детерминации значимо отличается от нуля. Для проверки этого выдвигается гипотеза:
1) Примем величину уровня значимости q = 0.05
2) Рассчитаем критерий проверки
^ R2 0.9348
-= 11671
(1 - R 2)/(N - 2) (1 - 0.9348)/814
F = ¦
3) Правило принятия решения
Принять Но, если F < F1-q,v1,v2.
В противном случае принять Н1 , то есть Н1 принимается, когда критерий проверки F попадает в критическую область
F > F1-q, v1,v2 '
F1- v1 v2 - это квантиль F -распределения, соответствующая уровню значимости q с ?1 = 1 степенями свободы для числителя и ?2 = N - 2 степенями свободы для знаменателя.
4) Расчет границ критической области
F1-qv1,v2 = FРАСПОБР(qVlV2) = = FРАСПОБР(0.05,1, 814) = 3.85
5) Проверка гипотезы
Так как критерий проверки для коэффициента детерминации находится в критической области, мы принимаем гипотезу Н1.
146
Это означает, что при заданном уровне значимости изменения отклика у объясняются изменением фактора t.
10.5. Полоса неопределенности рассеяния эмпирических данных относительно линии регрессии.
f + e в произвольной точке t
Дисперсия случайной величины у вычисляется по формуле:
_2 _ 2 °f+e = °е
k=1
где _
сте = 0.313 N = 816 T = 407.5
N _
Z (tk - T)2 = 45 278140
k=1
В данном случае на большом диапазоне изменения t без существенной потери точности вторым и третьим слагаемым в
скобках можно пренебречь, то есть &f+e ~ С>2е .
Величина Лу = 2t1-q /2 ?<У f+е называется шириной полосы
неопределенности. Зададимся доверительной вероятностью P = 0.95 (q = 0.05). Тогда квантиль распределения Стьюдента равна
t1-q /2,? = СТЬЮДРАСПОБР(^?) =
= СТЬЮДРАСПОБР(0.05, 814) = 1.96 Ширина полосы неопределенности составит Лу = 2-1.96 • 0.313 = 1.226
Следовательно, с вероятностью P = 0.95 случайная величина у = f + е будет лежать в пределах:
f-Лу/2 < у < f + Лу/2
(0.005 t + 4.402) - 0.613 < у < (0.005 t + 4.402) + 0.613
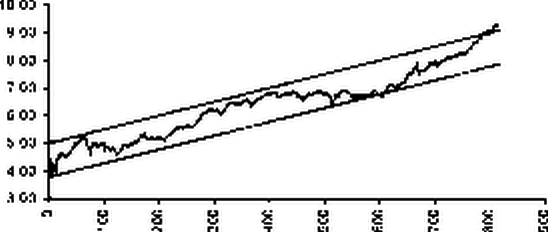
Эмпирическая зависимость и ее полоса неопределенности изображены на рисунке:
147
|
Эмпирическая зависимость и полоса неопределенности |
 |
|
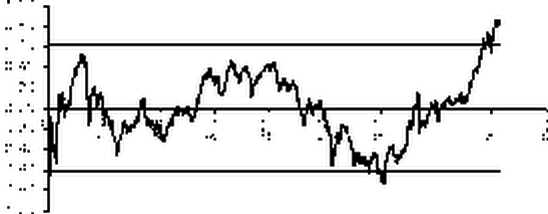
Ошибки линейной аппроксимации и полоса неопределенности |
 |
10.6. Проверка допущений МНК.
Для того, чтобы мы могли сказать, что модель адекватна эмпирическим данным, ошибки е должны обладать следующими свойствами:
1) Ошибки должны являться реализацией нормально распределенной случайной переменной.
2) Математическое ожидание ошибки должно быть равно нулю: M(ek ) = 0 .
148
Дисперсия ошибки должна быть постоянна: D(ek) = а2. Ошибки должны быть независимыми, то есть
3)
4)
cov(ek, e;)
Проверка гипотезы о том, что ошибки нормально распределены
Оценки основных параметров распределения величины е приведены в таблице:
|
Наименование оценки |
Величина |
|
Центр распределения e |
0.01 |
|
Среднеквадратичное отклонение a e |
0.313 |
|
Коэффициент асимметрии у |
0.063 |
|
С.к.о. коэффициента асимметрии а у |
0.085 |
Оптимальное число столбцов гистограммы можно найти, округлив вниз до ближайшего большего или равного пяти нечетного целого величину, определенную по формуле:
L = НІА N “
6
Вычисленное значение L = 9. Таким образом, область изменения величины е разбивается на 9 интервалов, в каждом из которых необходимо рассчитать эмпирические частоты попадания в соответствующий интервал.
При использовании критерия согласия Пирсона необходимо вычислить величину:
z2=і
i=1
где
L - количество столбцов гистограммы,
149
si - эмпирическая частота попадания в i-й столбец, Ti - теоретическая частота попадания в i-й столбец.
Приведем таблицу эмпирических частот.
|
Номер ин тервала |
|
Левая граница |
Правая граница |
Эмпирическая частота si |
|
|
1 |
-0.8732 |
-0.6791 |
5 |
|
|
2 |
-0.6791 |
-0.4851 |
46 |
|
|
3 |
-0.4851 |
-0.2911 |
87 |
|
|
4 |
-0.2911 |
-0.0970 |
166 |
|
|
5 |
-0.0970 |
0.0970 |
206 |
|
|
6 |
0.0970 |
0.2911 |
139 |
|
|
7 |
0.2911 |
0.4851 |
124 |
|
|
8 |
0.4851 |
0.6791 |
22 |
|
|
9 |
0.6791 |
0.8732 |
21 |
то несимметричность носит случайный характер и распределение частот можно расчетным образом симметрировать относительно центрального пятого столбца:
|
Номер ин тервала |
|
Левая граница |
Правая граница |
Эмпирическая частота si |
|
|
1 |
-0.8732 |
-0.6791 |
13.00 |
|
|
2 |
-0.6791 |
-0.4851 |
34.00 |
|
|
3 |
-0.4851 |
-0.2911 |
105.50 |
|
|
4 |
-0.2911 |
-0.0970 |
152.50 |
|
|
5 |
-0.0970 |
0.0970 |
206.00 |
|
|
6 |
0.0970 |
0.2911 |
152.50 |
|
|
7 |
0.2911 |
0.4851 |
105.50 |
|
|
8 |
0.4851 |
0.6791 |
34.00 |
|
|
9 |
0.6791 |
0.8732 |
13.00 |
150
|
Номер интервала |
|
Левая граница |
Правая граница |
Эмпирическая частота |
Теоретическая частота Ti |
(T - S )2 Ti |
|
|
1 |
-0.8732 |
-0.6791 |
13.00 |
10.03 |
0.88 |
|
|
2 |
-0.6791 |
-0.4851 |
34.00 |
37.08 |
0.26 |
|
|
3 |
-0.4851 |
-0.2911 |
105.50 |
94.29 |
1.33 |
|
|
4 |
-0.2911 |
-0.0970 |
152.50 |
165.03 |
0.95 |
|
|
5 |
-0.0970 |
0.0970 |
206.00 |
198.88 |
0.25 |
|
|
6 |
0.0970 |
0.2911 |
152.50 |
165.03 |
0.95 |
|
|
7 |
0.2911 |
0.4851 |
105.50 |
94.29 |
1.33 |
|
|
8 |
0.4851 |
0.6791 |
34.00 |
37.08 |
0.26 |
|
|
9 |
0.6791 |
0.8732 |
13.00 |
10.03 |
0.88 |
|
|
|
|
|
|
ИТОГО |
X2 = 7.09 |
Х1%,? = ХИ2ОБР(0.05, 6) = 12.59
Так как %г <Хі%?> то распределение отклонений от линии
регрессии можно аппроксимировать нормальным распределением при заданном уровне значимости.
Проверка гипотезы о том, что математическое ожидание ошибки равно нулю
Проверка гипотезы осуществляется по схеме:
1) Априорные предположения Математическое ожидание ошибки равно нулю
Me = 0
2) Результаты испытания
Выборочная средняя ошибки и выборочное с.к.о. ошибки
e=0.01
о e = 0.313
при объеме выборки N = 816.
3) Гипотеза
151
H 0 : e = 0 H1 : eФ 0
4) Принятая величина уровня значимости q = 0.05
5) Расчет критерия проверки
0.01
0.313
e -Ve
0.032
6)
7)
8)
Правило принятия решения
ПРинять Н0 , если - ti-q / 2, ? < t < t1-q / 2, V
В противном случае принять Н1.
Расчет границ критической области
t1-q/2,? = СТЬЮДРАСПОБР(q, N - 2) =
= СТЬЮДРАСПОБР(0.05, 814) = 1.96 Проверка гипотезы
Так как — t1-q /2 ? < t < t1- /2 ? то мы принимаем гипотезу Н0, то есть при заданном уровне значимости выборочная средняя
ошибки e статистически незначимо отличается от нуля.
Проверка гипотезы о том, что дисперсия ошибки постоянна
Для проверки этой гипотезы разделим эмпирические данные на две группы по 350 точек: с 1-й по 350-ю и с 467-й по 816-ю точки. Серединные точки с 351-й по 466-ю (14.2% от объема выборки) исключаем для лучшего разграничения между группами. Рассчитаем суммы квадратов ошибок для каждой из этих групп:
816 350
S = Z e; = 50.37 S = ? ek = 19.67
k=467 k=1
Проверка гипотезы о постоянстве дисперсии осуществляется по схеме:
1) Гипотеза
22
п 0 : ^1 _ ^2 H Г- S12 > S 22
2) Принятая величина уровня значимости
152
В противном случае принять НІ , то есть НІ принимается, когда критерий проверки F попадает в критическую область F > F1 — q,vUV2.
q = 0.01
Расчет критерия проверки
3)
4)
S1 50.37
= 2.561
S 2 19.67
Правило принятия решения Принять Н0, если F < F1
1—q, v1, v2
5)
Расчет границ критической области
F-qw2 = FРАСПОБР(q,Vl,v2) =
= FРАСПОБР(0.01, 350 — 2, 350 — 2) = 1.284
6) Проверка гипотезы
Даже при уровне значимости q = 0.01 критерий проверки
F попадает в критическую область F > F1— v1 ?2, то есть
мы отклоняем гипотезу Н0 и принимаем гипотезу Н . Следовательно дисперсия ошибок регрессии не постоянна.
Проверка гипотезы о том, что ошибки независимы
На практике проверяется не независимость, а некоррелированность ошибок, которая является необходимым, но недостаточным условием независимости. Для этого нужно рассчитать коэффициент автокорреляции первого порядка
^ ekek+1
k=1_
Pk, k+1
|
N—1 | |
 |
e |
|
N—1 | ||
|
2 k | 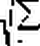 |
e 2 k +1 |
153
Выводы
Следует признать, что аппроксимация линейной функцией логарифма цены актива является неудовлетворительной, так как не соблюдаются два из четырех допущений МНК.
Не приводя доказательств скажем, что попытка уточнить модель путем введения циклических компонент не приводит к улучшению качества ошибок регрессии.
На практике при изучении динамических рядов цен активов используют методы адаптивного моделирования, о которых будет рассказано в следующих главах.