Анализ Фурье

9.1. Введение.

В этой главе излагается метод аппроксимации эмпирической зависимости тригонометрическим рядом Фурье. Даны формулы, позволяющие по реальной выборке вычислить коэффициенты Фурье, амплитуду и фазу гармоник. Рассказано, как строится амплитудно-частотная характеристика разложения, и как она используется для выделения гармоник с максимальной амплитудой.

9.2. Численный анализ Фурье.

Пусть выборка значений фактора Х и отклика Y задана в виде массива (x_n,y_n),n = 0,...,N, содержащего N +1 точку,

причем все значения фактора Х упорядочены по возрастанию и равноотстоят друг от друга. Будем считать, что величина Х изменяется в интервале (0, X_max ), следовательно выборка фактора

Х задается рядом x_n = X_max • n / N .

Если принято решение о том, что связь переменных Х и Y носит периодический характер, то аппроксимировать зависимость Y от Х на интервале (0, X_max ) необходимо тригонометрическим рядом, то есть функцией вида:

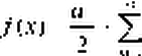
am cos m

2лх ' ₇ . ( 2лх

- + b_m sin m-

max J V max J

X ^m X

^ mov / V X\. )

Данная функция зависит от (2М+1) параметра (a₀,a₁,...,a_M,b₁,...,b_M) . Так как количество неизвестных параметров 2M +1 не должно превышать объем выборки N +1 , то M < N/2.

Наилучшим приближением будет тригонометрический ряд с таким набором параметров, который минимизирует сумму квадратов отклонений этого ряда от выборочных значений отклика Y, то есть

^S = Z ^[Уп ^{- f (x}n ^)]2 ^ ^min

n=1



Без доказательства приведем формулы для искомых параметров:

определения

2 ( 2 т Л

N

2wn

_т =—X y_n cos| m-I 0 < m < M

^N n=0 2 ^N—

^Ьт = N X Уп ЙПІ ^m— I 1 < ^m < ^M

Определенные по этим формулам параметры называют коэффициентами Фурье, а тригонометрический ряд с такими коэффициентами является рядом Фурье. Тогда аппроксимация величины Y рядом Фурье в точке x_n = X_max п / N будет равна:

a ^M

fn = ^a+X

² m=1

( 2m Л ₇ . ( 2m

a_m cos| m-I + b_m sin| m-

При увеличении количества гармоник М эта аппроксимация все точнее описывает выборочные значения величины Y, и наконец при M = N /2 для любого п становится справедливым

р^{авенство} Уп = ^fn.

Однако, наша задача состоит не в том, чтобы с абсолютной точностью аппроксимировать исходную выборку, то есть включить в математическую модель все наблюдающиеся особенности конкретной выборки, в том числе и те, которые в действительности носят случайный характер. Нам нужно найти всего несколько наиболее значимых гармоник, то есть гармоник, имеющих максимальную амплитуду. Для этого необходимо построить и проанализировать амплитудно-частотную характеристику разложения.

9.3. Амплитудно-частотная характеристика.

Введем параметры (R_m,?_т), которые назовем амплитуда и фаза соответственно. Эти величины связаны с параметрами (a_m, b_m ) следующими соотношениями:

^bm

-arctg—<sup>m

a</sup>m

^Rm =V ^al + ^bm ^am = ^Rm ^C0^m

?

m

^bm

R_m sin ?„

133

Тогда, заменив параметры (a_m, b_m ), разложение Фурье можно

переписать в виде

м

fn =

^-0

2

z

m=1

м

R_m cos ?_т cosl m

2m

- R_m sin ?„ sinl m

2m

2m _

m-+ ?„

f_n = — + Z R_m cosl

2 m=i [ n j

Назовем частотой колебаний величину о _m = m / N . Полный

набор частот называется спектром разложения. Тогда окончательно получаем a ^м

fn = -f +Z Rm

² m =1

Смысл приведенных выше преобразований состоит в том, чтобы перейти от ряда из синусов и косинусов к ряду из одних косинусов. Если теперь построить график, где по оси абсцисс отложена частота, а по оси ординат отложена амплитуда, то есть график в координатах (о _m, R_m ), то наглядно будет видно, при каких значениях частоты наблюдаются максимумы амплитуды. Такой график называется амплитудно-частотной характеристикой (АЧХ). С помощью АЧХ мы получаем возможность выбрать из разложения Фурье только самые значимые гармоники и пренебречь остальными. Заметим, что период колебания связан с частотой соотношением T_m = 1/ o_m.

При необходимости аналогичным образом можно построить фазочастотную характеристику (ФЧХ), то есть график в коорд^{инатах (о} m ?m ⁾ .

cos

((топ + ? _m)

mm

9.4. Пример выделения основной гармоники с помощью анализа Фурье.

Рассмотрим выделение основной гармоники с помощью анализа Фурье на примере выборки, состоящей из 256-ти точек (^хп,У_п),п = 0,...,255. График исходных данных приведен на рисунке.

134

б-.

¦ Исходные данные

4-

2-

¦¦¦Л

¦ ¦ ¦

.*ч* ?* ч

¦ ¦>*

<*

¦<г

-2-

-4-

¦Л#е

¦ ¦¦¦

¦ ¦ *>/¦

%^^?

« ¦

/л

¦ ¦¦% ¦

20^-4

¦ ²⁵ V* *\ ¦ <* П*

*?/

250

300

-б-І

Этот график дает основания предположить, что связь переменных Хи Y носит периодический характер. По методике, изложенной в предыдущих 2-х параграфах, представим аппроксимирующую функцию рядом Фурье и построим амплитудночастотную характеристику.

АЧХ


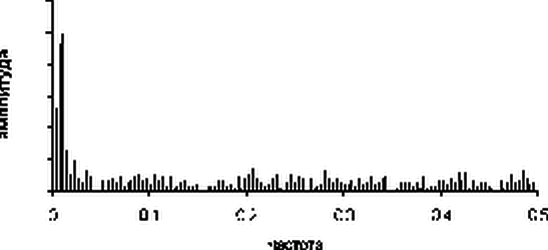
Максимум амплитуды находится в начальной части спектра. Рассмотрим подробнее этот участок.

135

АЧХ

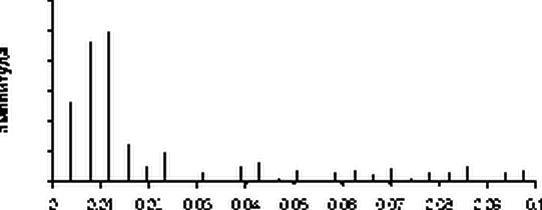
частота

При ближайшем рассмотрении оказывается, что максимум амплитуды приходится на частоту а ~ 0.01 (период T ~ 100). Учитывая, что а _m = m / N, рассчитаем для этого значения частоты коэффициенты разложения Фурье: ^am = ^a(Pm ⁾ = -°.¹⁰49 bm = b(a_m ) = -2.8918

Используя эти данные, вычисляем амплитуду и фазу основной гармоники:

Rm = 2.8934

?m = 1.6070

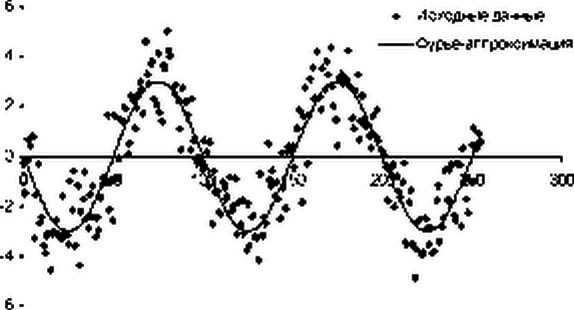
Таким образом, Фурье-аппроксимация исходных данных и

ошибки модели будут вычисляться по формулам

f_n = R_m cos(2n®_mn + ?_п )= 2.8934 • cos(2n- 0.01- n +1.607)

e = y - f

n У n J n

Приведем график исходных данных вместе с Фурье-аппроксимацией и график остатков (ошибок модели).

136

6-,

¦ Остатки

4-

¦ ¦ ¦ .







К *4 4«l V »\|» Ч~ $^fH ' *»4*%t4»* *»f⁴4l*

2

0

-2

-4-1

¦ > V»' ¦* »V.¦ >Л? ^т,г ¦ <

: У*⁴⁴ *¦ 30^*\ 4*0Ю^# ** ^5о % /200_#WV *250

І ¦ ¦¦ * ¦ « ¦ * 4 »4

4 ¦ ¦

300

-6

Очевидно, что ошибки аппроксимации носят непериодический характер. В противном случае нужно было бы повторить всю процедуру, используя в качестве исходной выборки эти ошибки, и повторять ее до тех пор, пока не будут выделены все значимые гармоники.

Па практике, при изучении динамики цен активов не рекомендуется использовать для аппроксимации этих рядов более трех гармоник Фурье.



Содержание раздела

---