Регрессионный анализ

8.1. Введение.

Различные экономические и финансовые переменные связаны между собой. Если не принимать во внимание случайный характер этих переменных, то для описания связей между ними можно применить функциональный подход, то есть предположить, что связь одной из переменных Y с некоторым количеством других переменных (X_x,...,X_M) можно выразить некоторой функцией (математической моделью):

^Y = ^{f (a}i,..., ^aL,^Xi,..., ^Xm ^ где

- (X_1v.., X_M) - это набор независимых переменных, которые будем называть факторами,

- Y - это зависимая переменная, которую будем называть откликом,

^{- (a}iv.., ^aL^{) - это} набор констант, которые будем называть параметрами математической модели.

В случае, когда отклик Y зависит только от единственного фактора Х, модель называется однофакторной. Если отклик Y зависит от нескольких факторов (X₁,..., X_M), модель называется многофакторной.

Математическая модель, связывающая факторы и отклик, может быть найдена только на основе реальных выборок этих величин. Определение модели включает в себя два этапа:

- выбор вида модели, то есть вида функции f,

- расчет параметров выбранной модели (a₁,..., a_L ).

Первый этап, то есть выбор вида математической модели, является не формализуемой задачей. Это решение принимается с учетом простоты и удобства использования модели, содержательности модели и других соображений. Второй этап, то есть расчет параметров выбранной математической модели, является задачей, которая решается с помощью регрессионного анализа реальных выборок факторов и отклика.

8.2. Выбор вида математической модели.

Рассмотрим однофакторную зависимость. Этот случай наиболее прост и может быть изучен графически. Предположим,



что имеется массив значений фактора Х и соответствующий ему массив значений отклика Y. Нанесем соответствующие точки (^хк,Ук),к = 1,...,N на график. Если фактор и отклик - это реальные статистические данные, то указанные точки никогда не лягут на простую линию (прямую, параболу, гиперболу, экспоненту, синусоиду и т.д.). Всегда будут присутствовать отклонения, связанные со случайным характером рассматриваемых переменных и/или с влиянием неучтенных факторов.

Кроме того часто оказывается, что один и тот же набор точек можно с примерно одинаковой точностью описать различными аналитическими функциями. Следовательно, выбор вида математической модели - это не формализуемая задача. Рациональный выбор той или иной модели может быть обоснован лишь с учетом определенных требований, а именно:

- простоты модели,

- содержательности модели.

Простота модели

Наиболее распространенной ошибкой при описании фактической зависимости является попытка детерминированного описания этой зависимости, то есть включение в математическую модель всех наблюдающихся особенностей конкретной выборки, в том числе и тех, которые в действительности носят случайный характер.

Например, любой набор точек (х_к,у_к),к = 1,...,N можно описать абсолютно точно полиномом (N-l')-w. степени, зависящим от N параметров (а₀, a₁,..., a_N_₁):

N _1

у = Z ^ак^хк

к=0

Но на практике получается, что появляющаяся новая (Ы+Г)-я точка уже не будет удовлетворять полученной формуле. То же самое можно сказать обо всех появляющихся далее новых точках. При этом расхождение между реальными данными и моделью будет нарастать с увеличением количества новых данных.

В то же время может оказаться, что исходный набор значений (х_к, у_к) можно приближенно описать какой-либо простой функцией (прямой, параболой, гиперболой, экспонен

102

той, синусоидой и т.д.), и эта модель, зависящая от небольшого числа параметров, будет устойчива к появлению новых данных. Следовательно, необходимым требованием к математической модели является ее простота.

Содержательность модели

Под содержательностью математической модели будем понимать разумную интерпретируемость результатов, которые могут быть получены при вычислении по этой модели.

Поясним это утверждение на простом примере. Пусть наша задача состоит в том, чтобы описать кривую зависимости цены бескупонной облигации от срока до погашения облигации. В данном случае фактором X является срок до погашения, откликом Y является цена. На эту математическую модель можно наложить очевидные ограничения:

1) функция y = f (х) должна быть неотрицательной,

2) функция y = f (х) должна быть монотонно убывающей,

3) значение функции y = f (х) при х = 0 должно быть равно константе (номиналу облигации),

4) значение функции y = f (х) при х ^ ж должно стремиться к нулю.

Приведем примеры функций, которые не удовлетворяют хотя бы одному из ограничений и поэтому не могут быть использованы для построения рассматриваемой модели из соображений содержательности:

- линейная функция y = b — ах не удовлетворяет первому и четвертому условию, так как при х ^ ж величина y ^ —ж ,

- гипербола y = b + а / х не соответствует третьему условию, так как при х ^ 0 величина y ^ ж .

При этом данные функции могут удовлетворительным образом описывать набор исходных данных (х_к, y_k ) .

8.3. Расчет параметров математической модели.

Если выбор вида математической модели - это не формализуемая задача, то расчет параметров уже выбранной математической модели является чисто формальным процессом. В общем

103

случае он состоит в решении системы вообще говоря нелинейных уравнений.

Рассмотрим произвольную однофакторную зависимость, то есть модель, в которой связь фактора Х и отклика Y выражается функцией Y = f(a₁,...,a_L,X). Вид функции предполагается известным. Наша задача состоит в том, чтобы по имеющейся выборке данных, то есть по набору точек (х_к,у_к),к = 1,...,N

вычислить неизвестные параметры модели (a₁,...,a_L). Для этого нам нужно решить систему уравнений:

Уі = ^{f (a}i,-, ^aL ^{, X}l⁾

< Ук = ^{f (a}i,-, ^a L ^{, X}k ⁾

Xn = ^{f (a}i,-, ^aL ^{, X}N ⁾

Эта система состоит из N уравнений с L неизвестными параметрами модели (a₁,...,a_L). Возможны три варианта соотношения между количеством уравнений N и количеством неизвестных L:

1) N < L

В этом случае объем выборки является недостаточным для определения параметров модели. Необходимо увеличить количество фактических данных и/или упростить модель, уменьшив количество ее параметров.

2) N = L

Если объем выборки совпадает с количеством неизвестных параметров, то решение системы единственно. Но так как предполагается, что исходные данные (х_к, у_к ) могут иметь

случайный характер, то и решение (a₁,..., a_L ) также случайно, так как оно в точности соответствует случайным исходным данным.

3) N > L

При объеме выборки, превышающем количество неизвестных параметров, система уравнений является избыточной. Из исходной системы уравнений в различных комбинациях можно составить несколько систем по L уравнений в каждой. Каждая

104

из систем даст свое решение, и все эти решения будут вообще говоря разными. Если их нанести на график, то получится целый пучок аппроксимирующих кривых. Если эти кривые каким-либо образом усреднить, то полученное усредненное решение будет гораздо достовернее описывать истинную зависимость между Х и Y, так как оно в значительной степени будет защищено от случайности выборки. Этот эффект усреднения тем больше, чем больше объем выборки N.

Наиболее эффективным методом усреднения решений избыточной системы уравнений является регрессионный анализ или метод наименьших квадратов (МНК).

8.4. Сущность метода наименьших квадратов.

Пусть после предварительного анализа принято решение о том, что связь фактора Х и отклика Y выражается функцией Y = f(a_1v..,a_L,X). Наша задача состоит в том, чтобы по имеющейся выборке, то есть по набору точек (^хк,Ук),k = l,...,N вычислить наилучшие оценки неизвестных

параметров модели (a₁,...,a_L). Заметим, что все значения (^хк, У_к ) - это не переменные, а конкретные числа.

Между рассчитанными по модели значениями отклика f_k и реальными значениями из выборки У_к будут присутствовать расхождения, которые обозначим как

^ек = Ук - ^fk = Ук - ^f ^IV, ^aL , ^хк ⁾

Метод наименьших квадратов позволяет найти такой набор параметров модели, при котором сумма квадратов всех расхождений между значениями по выборке и вычисленными по модели значениями будет минимальной, то есть

N

S = 2 4 ^ min

к=1 N

^S = 2^[Ук ^{- f (a}1^,-_> ^aL , ^Хк ^)]2 ^ ^тІП

к=1

Величина S является функцией от L переменных (a₁,..., a_L ) . Минимум этой функции можно найти, приравняв к нулю все ее

105

частные производные по каждому из неизвестных параметров и решив полученную таким образом систему из L уравнений:

df ^(ai,..., ^aL, x_k⁾

da₁

dS

— =^-2Z^[ Ук - ^f («!>•••> ^aL ^{, X}k )]

da

к=1

dS JL df(a₁,..., a_L, x_k)

da

da_L

= -2^[Ук -f(ai,...,aL,Xk)]- ^{1 L}

к=1

Решение такой системы уравнений в случае нелинейной зависимости между Х и Y может быть сопряжено со значительными трудностями. Поэтому в дальнейшем мы ограничимся рассмотрением линейной зависимости между Х и Y, то есть линейной регрессии. К тому же, во многих случаях нелинейная зависимость может быть сведена к линейной достаточно простыми преобразованиями данных.

8.5. Свойства ошибок метода наименьших квадратов.

Рассмотрим подробнее ошибки, возникающие при применении МНК, то есть расхождения между рассчитанными по модели значениями отклика f _к и реальными значениями из выборки

У_к , которые мы обозначили как ^ек = Ук ^{- f}k = Ук ^{- f (a}iv, ^aL , ^Xk ⁾

Для того, чтобы мы могли сказать, что модель адекватна эмпирическим данным, эти ошибки должны обладать определенными свойствами:

1) Ошибки должны являться реализацией нормально распределенной случайной переменной.

Это означает, что хотя существует только один главный фактор Х, определяющий поведение отклика Y, но присутствует также большое количество малосущественных факторов, совокупное воздействие которых на отклик Y согласно центральной предельной теореме имеет нормальное распределение.

2) Математическое ожидание ошибки должно быть равно нулю: M(e_k ) = 0.

106

Это означает, что отсутствует систематическая ошибка в определении линии регрессии, следовательно оценки параметров регрессии являются несмещенными, то есть математическое ожидание оценки каждого параметра равно его истинному значению.

3) Дисперсия ошибки должна быть постоянна: D(e_k ) = а².

Это означает, что при увеличении объема выборки дисперсия оценок параметров регрессии стремится к нулю, то есть оценки параметров регрессии являются состоятельными.

4)

Ошибки должны быть независимыми, то есть

cov(^ek, ^ej⁾

Это означает, что ошибка в одной из величин отклика Y не приводит автоматически к ошибкам в последующих величинах.

Кроме того, в МНК предполагается что факторы (независимые переменные) не являются случайными величинами.

8.6. Оценка параметров однофакторной линейной регрессии.

Допустим, что принята гипотеза о том, что связь фактора Х и отклика Y выражается линейной функцией f (х) = ax + b . Наличие отклонений, связанных со случайным характером рассматриваемых переменных и/или с влиянием неучтенных факторов приведет к тому, что связь между рассчитанными по модели значениями отклика f_k и реальными значениями из выборки y_k будет выражаться в виде:

Л = ^fk + ^ek = ^axk + ^b + ^ek

где e_k - это расхождения между моделью и выборкой.

Оценка параметров линейной регрессии

Вычислим такой набор параметров модели, при котором сумма квадратов всех расхождений между значениями по выборке и вычисленными по модели значениями будет минимальной, то есть

107

N

S = Z ^el ^ ^min

к=1 N

^S = Z ^[Ук^{- ax}k^{- b}T ^ ^min

к=1

Величина S является функцией от 2-х переменных (a, b). Минимум этой функции можно найти, приравняв к нулю ее частные производные по каждому из неизвестных параметров и решив полученную таким образом систему из 2-х уравнений. Так как вычисление параметров мы будем проводить по конечной выборке, то в результате мы получим лишь оценку этих параметров (a, b):

dS_

db

dS_

da

N

²2^[Ук ^-axk ^-b] = ⁰

к=1

N

-²Z^[ Ук^{- ax}k^{- b]x}k =⁰

к=1

Из 1-го уравнения системы получаем:



Z Ук^{- a}Z ^xk^{- bN}=⁰ ^^b=^{Y - a} •^X



Из 2-го уравнения системы получаем:

N N N N N _ _



к=1 к=1 к=1 к=1 к=1

Подставив в это уравнение выражение для оценки параметра найдем оценку параметра a :

NN

Z ЗД - N • X • Y

к=1_

^N —2

Zxl -N-X

к=1

Z^(xk^{- X)(}Ук^{- Y)}

к=1

N

Z (xk - X )²

к=1

a=

Из последнего равенства следует, что оценку параметра a можно выразить через ковариацию или коэффициент корреляции переменных Х и Y:

108

'' ху 'у

a = —^ = р^-

'x ^'x

Параметр a, который еще называют коэффициентом регрессии, численно равен тангенсу угла наклона прямой регрессии к оси х.

Дисперсия оценок параметров линейной регрессии

Так как оценки параметров линейной регрессии получены по случайной выборке, то сами эти оценки являются случайными величинами. Оценка дисперсии параметра а выражается формулой:

'а N

k=1

где величина ' - это оценка дисперсии случайных отклоне

ний отклика Y от линии регрессии:

N - m -1 k=i

где m - число факторов (независимых переменных). В случае парной линейной регрессии

N

/ el =-

/ (Ук - ах, - Ъ)

N - 2 ^к N - 2 {= ^{k k}

1

Так как Ъ = Y - а • X и так как фактор Х предполагается нестохастическим, то для оценки дисперсии параметра Ъ справедливо:

' =' + ^Х •'а'

где величина 'y - это оценка дисперсии среднего значения отклика Y:

-2 1 -2

'^Y = N '^е

После несложных преобразований для оценки дисперсии параметра Ъ получаем формулу:

109

—2 У

-2 а

x,_r

k-1

^ab - N

У (x,. - X)^{2 N}

k-1

Величину a_e называют еще необъясненной дисперсией.

Чем меньше необъясненная дисперсия (то есть чем меньше отклонения величины Y от линии регрессии), тем меньше ошибки в определении параметров регрессии, и, следовательно, тем точнее модель объясняет фактические данные.

Кроме того, из формул для дисперсии параметров следует, что чем на более широком диапазоне изменения фактора Х оценивается регрессия, тем больше величина У (x_k — X)², а значит меньше дисперсия параметров.

Из тех же самых соображений следует, что чем больше объем выборки N, тем меньше дисперсия параметров.

8.7. Коэффициент детерминации.

Из того, что связь фактора Х и отклика Y выражается в виде

У, ^{- f}k + ^ek ^{- ax}k + ^b + ^ek

следует, что разброс отклика Y может быть объяснен разбросом фактора Х и случайной ошибкой е. Необходимо определить индикатор, который бы показывал, насколько разброс Y определяется разбросом Х и насколько случайными причинами, то есть насколько хорошо фактические данные описываются функцией регрессии.

В качестве общей меры разброса переменной Y естественно использовать сумму квадратов отклонений этой величины от ее среднего значения. Тогда в качестве объясняемой регрессией меры разброса переменной Y будем использовать сумму квадратов отклонений прогнозируемых линией регрессии значений от среднего значения величины Y.

Индикатором качества линии регрессии является коэффициент детерминации:

110

Z(/, - Y)² Z(ax, + b - Y)²

k=1

k=1

Z (Л - Y )² Z (y, - Y)²

k=1

k=1

или

Z

k=1

R² =1-

z (y, - y )²

k=1

В случае однофакторной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции величин Х и Y.

Иногда при расчете коэффициента детерминации для получения несмещенных оценок дисперсии в числителе и знаменателе делается поправка на число степеней свободы, то есть скорректированный коэффициент детерминации вычисляется по формуле:

N

1 ^{N 1}— Z

m - 1 k =1

R² =1-

Y )²

1Z⁽y,^-

¹ k=1

N - k=

где m - число факторов (независимых переменных).

При добавлении в уравнение регрессии дополнительных объясняющих переменных (факторов) нескорректированный R² всегда растет. При этом скорректированный R² может уменьшиться за счет увеличения числа m , если новый фактор приводит к небольшому уменьшению необъясненной дисперсии.

В случае парной линейной регрессии скорректированный

R ² вычисляется как:

₁N

Z<

k=1

R² =1 -

Y)²

і Z⁽у,^-

¹ k=1

N-

іи

Коэффициент детерминации может принимать значения от нуля (когда Y не зависит от Х) до единицы (когда Х полностью определяет Y, то есть между ними существует строгая функциональная зависимость). Чем больше этот коэффициент, тем выше качество линии регрессии.

Запишем формулу для R² в компактном виде

_R2_, —

" f

Отношение ширины полосы рассеяния данных относительно их среднего значения к ширине полосы рассеяния данных относительно линии регрессии называется числом различимых градаций отклика. Если в качестве меры рассеяния принять соответствующие среднеквадратичные отклонения, то формула для числа различимых градаций отклика будет иметь вид:

^NGRAD = ^—y / ^—e

Как и коэффициент детерминации, число различимых градаций является позитивной оценкой корреляционной связи, то есть чем больше N_GRAD, тем выше качество уравнения регрессии.

R² = 1 -1/ (grad )²

Негативной оценкой корреляционной связи является относительная приведенная погрешность, которая является отношением половины ширины полосы рассеяния данных относительно линии регрессии к ширине полосы рассеяния данных относительно их среднего значения и вычисляется по формуле

Y = 0.5 —-, то есть R² = 1 - (2у)².

^—У

N_g

Связь между у и N_grad задается формулами 11

GRAD

Приведем таблицу, показывающую связь между коэффициентом детерминации, числом различимых градаций отклика и относительной приведенной погрешностью.

112

N 1У GRAD	Y	R2	R
1	50.0%	0.00	0.00
1.41	35.4%	0.50	0.71
2	25.0%	0.75	0.87
3	16.7%	0.89	0.94
4	12.5%	0.94	0.97
5	10.0%	0.96	0.98
6	8.3%	0.972	0.986
7	7.1%	0.980	0.990
8	6.3%	0.984	0.992
9	5.6%	0.988	0.994
10	5.0%	0.990	0.995

Отметим следующие важные случаи:

- Коэффициент детерминации R² = 0.5 (R & 0.71), то есть только половина разброса отклика Y объясняется уравнением регрессии. В этой ситуации говорят, что влияние сигнала (фактора Х) равно влиянию помехи (случайной ошибки е). Поэтому при коэффициенте детерминации меньше чем 0.5, помехи начинают вносить основной вклад в вариацию переменной Y, и такая модель регрессии должна быть отвергнута.

- Если с.к.о. ошибки е ровно в два раза меньше, чем с.к.о. отклика Y, то есть число различимых градаций отклика равно

2, то R² = 0.75 (R & 0.87). Именно это значение рекомендуется принять в качестве минимально приемлемого значения коэффициента детерминации.

ПРИМЕЧАНИЕ. При оценке величин у и N_GRAD мы предполагали, что мерой ширины полосы рассеяния данных относительно их среднего значения и мерой ширины полосы рассеяния данных относительно линии регрессии являются соответствующие среднеквадратичные отклонения. Если в качестве меры принять доверительные интервалы, то формулы для у и N_GRAD изменятся, так как

отклик Y и ошибка уравнения регрессии е - это случайные величины с вообще говоря различными законами распределения. Рас

113

пределение величины Y, особенно при ярко выраженной линейной зависимости, близко к равномерному. Распределение величины е в большинстве случаев близко к нормальному.

8.8. Необратимость решений МНК.

Если отвлечься от причинно-следственной связи и рассматривать переменные Х и Y как равноправные, то по методу наименьших квадратов можно найти линейную регрессию как Y по X так и Х по Y.

Пусть линейная регрессия Y по X выражается функцией Y = a₁ X + Ъ_х, а линейная регрессия Х по Y функцией X = a₂Y + Ъ₂. Оценки параметров a_x и a₂ выражаются через коэффициент корреляции между переменными Х и Y как:









к=1

N

S⁽x^{- X)(}Ук^{- Y)}





к=1

Тангенс угла наклона функции Y = a₁ X + Ъ_: к оси х равен a_: = р ¦ (a_y /a _x), а тангенс угла наклона функции X = a₂Y + Ъ₂ к оси х равен 1/ a₂ = (1/ р) ¦ (a_y / a_x). Это разные величины, следовательно линии регрессии Y на Х и Х на Y - это разные прямые. Они совпадают только тогда, когда модуль коэффициента корреляции | р |= 1, то есть когда между переменными Х и Y существует строгая функциональная зависимость.

В несовпадении линий регрессии Y на Хи Х на Y и состоит необратимость решений МНК, то есть нельзя использовать величины (a₂ , Ъ₂ ) для вычисления величин (a₁ , Ъ₁ ) и наоборот:

1 a1 Ф— a2	7 Ъ2 Ъ1 Ф—- a2	1 a2 Ф — a1	Ъ1 Ъ2 Ф a1
		114

8.9. Статистические выводы о величине параметров однофакторной линейной регрессии.

Полученные в этой главе формулы для выборочных коэффициентов однофакторной линейной регрессии дают лишь оценки истинных значений этих коэффициентов.

Введем обозначения:

- истинные значения параметров линейной регрессии (a, Ь),

- выборочные значения параметров линейной регрессии

(a, Ь),

выборочные дисперсии параметров (a_a ,а_ь ) .

Выборочное распределение параметров линейной регрессии При анализе коэффициентов регрессии считают, что

случайные величины t_a = ¦

и tb =

подчиняются

распределению Стьюдента с V = (N — 2) степенями свободы, где N - объем выборки. В этих формулах:

Е^(Хк^{— x)(}Ук <sup>— Y)

Ь</sup> = Т7Е Ук ^{— a}Tr Е

к=1

X,,

N к =1

Е (^хк—x )²

к=1

к=1

а„

а„

^а a N

Е (Хк — X)

к=1

-2 1

=

Хи

Е (^хк — x)

к=1

Е⁽Ук^—ихк^—Ь)

N — 2 к=1

Доверительный интервал для параметров линейной регрессии

Доверительный интервал возможных значений величины t, характеризующийся доверительной вероятностью P или уровнем значимости q = 1 — P , это такой интерквантильный

115

промежуток t_q/2? < t < t_{1—q/2 v}, внутри которого лежат 100P процентов всех значений случайной величины t, а 100q процентов лежат вне этого промежутка. При этом 100q /2 процентов лежит слева от t_q/2? и 100q/2 процентов лежит

^спр^ава ОТ ^t1_q / 2, ? .

Величины t_q/2? и t_1-q/2? - это квантили распределения

Стьюдента с ? = N — 2 степенями свободы, причем, так как это распределение симметрично и имеет нулевое математическое

^ожид^ание, ^{то t}q / 2, ? = ^—t1—q/2,? .

Подставив значения t_a = (a — a) / u_a и t_b = (b — b)/a_b в двойное неравенство — t_{1—q /2 ?} < t < t_{1— /2 ?} получим

доверительные интервалы для истинных значений параметров линейной регрессии (a, b):

^{a — t}1—qп?°а < ^a < ^a + ^t1—q/2,?^аа ^{b — t}1—q ,Х?°Ь < ^b < ^b + ^t1—q ,Х?°Ь

Гипотезы о величине параметров линейной регрессии

Когда речь идет о линейной регрессии, необходимо знать, насколько значимо отличаются от нуля величины параметров регрессии. Для проверки этого выдвигаются гипотезы:

H 0: a = 0 H 0 : b _ или H : a Ф 0 H1 : b

b = 0

Проверка данных гипотез осуществляется в отдельности для каждого из параметров по следующей схеме:

1) Априорные предположения

Истинные значения параметров регрессии равны нулю a = 0

b = 0

2) Результаты испытания

Выборочные коэффициенты регрессии и их выборочные с. к. о.

116

a, О

^Ь,ОЬ

при объеме выборки N.

3) Гипотеза

H 0:	a = 0		H 0 :	о ll
_	или
H :	a Ф 0		H :	Ь Ф 0

4) Принятая величина уровня значимости q = 0.05 или q = 0.01

5) Критерий проверки _t = Ь-Ь=_Ь_

^{Ь О}ь ^Оь

6) Правило принятия решения

Пр^инЯ1Ъ ^Н0 , ^{если - t}i_q _П? < ^t < ^ti_q_/2>v

В противном случае принять Н₁ , то есть Н₁ принимается, когда критерий проверки t попадает в критическую область

I ^t I > ^t1-q/2, V .

Граница критической области вычисляется как t_1-q/2,_V = СТЬЮДРАСПОБРІД, N - 2)

В качестве критерия проверки t используются t_a и t_b .

7) Проверка гипотезы

- Если - t_{1-q /2 V} < t < t_{1- /2 V} то критерий проверки t не попадает в критическую область и мы принимаем гипотезу Н₀. Это означает, что при заданном уровне значимости соответствующий параметр регрессии статистически незначимо отличается от нуля.

- В противном случае мы принимаем гипотезу Н₁ . Это означает, что при заданном уровне значимости соответствующий параметр регрессии статистически значимо отличается от нуля.

117

8.10. Статистические выводы о величине коэффициента детерминации.

Коэффициент детерминации является индикатором того, насколько хорошо изменения фактора X объясняют изменения отклика Y. Чем он ближе к единице, тем выше качество уравнения регрессии.

Так как коэффициент детерминации вычисляется по конечной случайной выборке, то он сам является случайной величиной. Проверка значимости коэффициента детерминации -это проверка гипотезы о том, что он значимо отличается от нуля.

H ₀ :

H : R² > 0

Критерий проверки рассчитывается по формуле:

^ R²/ m

F =-₂-

(1 - R²)/(N - m -1)

где N - объем выборки, m - количество независимых переменных (факторов). Критерий проверки подчиняется F -распределению с m степенями свободы для числителя и (N - m - 1) степенями свободы для знаменателя.

В случае однофакторной линейной регрессии критерий проверки принимает вид:

R²

(1 - R²)/(N - 2)

Количество степеней свободы для числителя равно 1, количество степеней свободы для знаменателя равно (N - 2) .

Если в действительности переменная Y не зависит от переменной X , то коэффициент детерминации R² и критерий проверки F равны нулю. При этом их оценки по случайной выборке могут отличаться от нуля, но чем больше это отличие, тем менее оно вероятно.

Если же критерий проверки F больше некоторого критического значения при заданном уровне доверительной вероятности, то это событие считается слишком маловероятным

118

и мы отвергаем гипотезу H₀ и принимаем гипотезу H₁ . Это

значит, что переменная Y зависит от переменной X .

Проверка гипотезы для однофакторной линейной регрессии проводится по следующей схеме:

1) Гипотеза

H ₀: R² = 0

H₁ : R² > 0

2) Принятая величина уровня значимости q = 0.05 или q = 0.01

3) Критерий проверки

R 2

F =-- (N - 2)

1 - R²

4) Правило принятия решения Принять Но, если F < F_1-q,_?1,_?2.

В противном случае принять Н₁, то есть Н₁ принимается, когда критерий проверки F попадает в критическую область

^F > ^F1-q, v1,v2 .

Здесь F_{1-q v1 v2} - это квантиль F -распределения, соответствующая уровню значимости q с ?₁ = 1 степенями свободы для числителя и ?₂ = N — 2 степенями свободы для знаменателя.

Величину F_{1—q ?1 ?2} можно вычислить с помощью электронных таблиц Microsoft Excel:

Fi-q.vi.v2 = FРАСПОБР(q,Vl,?₂)

5) Проверка гипотезы

- Если F < F_{1— v1 ?2}, то критерий проверки F не попадает в

критическую область и мы принимаем гипотезу Н₀. Это означает, что при заданном уровне значимости изменения фактора X не объясняют изменения отклика Y и регрессионная модель должна быть отвергнута.

- В противном случае мы принимаем гипотезу Н₁ . Это означает, что при заданном уровне значимости переменная Y зависит от переменной X .

119

8.11. Полоса неопределенности однофакторной линейной регрессии.

Так как параметры линейной регрессии зависимы между собой (b = Y - a ¦ X), то уравнение регрессии можно переписать в виде f = ax + b = a ¦ (x - X) + Y. Каждая точка на

линии регрессии выражается через выборочные значения (a, Y),

имеющие выборочные дисперсии (a_a ,аа ), и потому является случайной величиной.

Дисперсия линии регрессии

Так как в МНК предполагается, что фактор Х нестохастичен, то дисперсию точки на линии регрессии можно выразить следующим образом:

а/ =^(x-^X)2 ¦ст/ +а/

Из этой формулы следует, что:

- дисперсия величины Y влияет на дисперсию точки на линии регрессии аддитивным образом, то есть ее вклад постоянен и не зависит от величины фактора Х,

- дисперсия величины a влияет на дисперсию точки на линии регрессии мультипликативным образом, то есть ее вклад тем больше, чем больше абсолютное отклонение фактора Х

от X .

С учетом того, что

а„

Z (X» - X)²

для дисперсии точки на линии регрессии получим:

С \

^af =°е

Z (X» - X)²

»=1

120

Доверительный интервал линии регрессии

Аналогично тому, как мы нашли доверительные интервалы для истинных параметров линейной регрессии, мы можем записать доверительный интервал для линии регрессии в виде:

^{f — t}1—qn,v°f ^{— f — f} + ^t1—qn,v°f

Ширина доверительного интервала линии регрессии равна 2t_{l-q/2 v}o_f . Эту величину называют еще шириной полосы неопределенности линии регрессии.

8.12. Прогнозирование на основе однофакторной линейной регрессии.

При прогнозировании, то есть при экстраполяции линии регрессии за пределы поля точек, по которым была получена эта линия, мы должны учитывать не только неопределенность положения самой линии регрессии (о чем говорилось в предыдущем параграфе), но и дисперсию случайных отклонений от нее (ошибок МНК).

Дисперсия прогноза

Дисперсию случайной величины y = f + e в произвольной

точке х можно выразить следующим образом:

-2 -2 -2

®f+e = ®f + ®e

Используя полученную в предыдущем параграфе формулу для дисперсии линии регрессии получаем:

С \

^Gf+e = ® e

I (- X)² к=1

Доверительный интервал прогноза

Так как математическое ожидание ошибки МНК е равно нулю, то доверительный интервал для прогнозного значения отклика Y в точке х определяется неравенствами:

^{f — t}1-q/2,v® f+e — У — ^f + ^t1-q/2, v® f+e ¦

121

шириной полосы

Назовем величину Ay = 2 t_1—/2v&f+_e неопределенности прогноза.

Горизонт прогнозирования

Ширина полосы неопределенности прогноза минимальна при X = X и возрастает при увеличении абсолютной величины

отклонения переменной х от X. Точность прогноза определяется шириной полосы неопределенности.

Пусть мы априорно задаем максимально возможную ширину неопределенности прогноза Ay_max и считаем, что точность прогноза является удовлетворительной, если в точке прогноза Ay < Ay_max. При удалении от поля точек, по которым была получена линия регрессии, Ay обязательно достигнет Ay_max.

Соответствующее удаление называется горизонтом прогнозирования. Дальнейшее удаление приведет к тому, что Ay превысит Ay_max. Интервал значений х, в пределах которого

точность прогноза неравенством:

является

удовлетворительной,

выражается

(а V

^Ay_max_

^ ^2t1-q/2, v®e J

Z (X, - X)²

где

x„

k=1

8.13. Проверка допущений МНК.

Изучая уравнение линейной регрессии мы предполагали, что реальная взаимосвязь фактора Х и отклика Y линейна, а отклонения от прямой регрессии случайны, независимы между собой, имеют нулевое математическое ожидание и постоянную дисперсию. Если это не так, то статистический анализ параметров регрессии некорректен и оценки этих параметров не обладают свойствами несмещенности и состоятельности. Например, это может быть, если в действительности связь между переменными нелинейна. Поэтому после получения уравнения регрессии необходимо исследовать его ошибки.

122

Ошибки метода наименьших квадратов, то есть величины e_k = y_k — f_k должны обладать следующими свойствами:

1) Ошибки должны являться реализацией нормально распределенной случайной переменной.

2) Математическое ожидание ошибки должно быть равно нулю: M (e_k ) = 0 .

3)

4)

Дисперсия ошибки должна быть постоянна: D(e_k) = о². Ошибки должны быть независимыми, то есть

^{0 k} * j °^{2 k} = j

cov^(ek, ^e;⁾

После того, как получено уравнение регрессии y = ax + b + e , каждое из этих допущений должно быть проверено.

Проверка гипотезы о том, что ошибки нормально распределены

Идентификация закона распределения случайной величины изучена в главе 6, поэтому здесь мы не будем подробно рассматривать этот вопрос. Кратко можно сказать, что проверка гипотезы о том, что ошибки МНК нормально распределены, проводится в два этапа:

1) По выборке (e₁,e₂,...,e_N) строится гистограмма

распределения случайной величины е.

2) Полученная гистограмма проверяется на соответствие нормальному распределению с помощью критерия согласия Пирсона.

Проверка гипотезы о том, что математическое ожидание ошибки равно нулю

Пусть ошибка МНК е имеет математическое ожидание jU_e и генеральную дисперсию о²е. Состоятельными и несмещенными

оценками математического ожидания и дисперсии ошибки будут выборочная средняя и выборочная дисперсия:

- 1 ^N - -^e = N ?⁽yk^{- ax}k<sup>- b)

N</sup> k=1

123

_₂ 1 ^N - -

o_e =-У (y_k - ^ахк - b)

^e N - 2

Мы должны проверить гипотезу H ₀ : e = 0

H₁ : e Ф 0

Проверка этой гипотезы осуществляется по следующей схеме:

1) Априорные предположения Математическое ожидание ошибки равно нулю

Me = ⁰

2) Результаты испытания

Выборочная средняя ошибки и выборочное с.к.о. ошибки

^ ⁰ e

при объеме выборки N.

3) Гипотеза

H ₀: e = 0 H₁ : eФ 0

4) Принятая величина уровня значимости q = 0.05 или q = 0.01

5) Критерий проверки

t=h* =L

о о

ee

6) Правило принятия решения

^Пр^{инять Н}0, ^{если - t}1-q 12, V < ^t < ^t1-q / 2, V

В противном случае принять Н₁, то есть Н₁ принимается, когда критерий проверки t попадает в критическую область

I ^t I > ^t1-q/2, V .

7) Проверка гипотезы

- Если - t_{1-q /2 V} < t < t_{1-q /2 V} то критерий проверки t не попадает в критическую область и мы принимаем гипотезу Н₀. Это означает, что при заданном уровне значимости выборочная

средняя ошибки e статистически незначимо отличается от нуля.

124

- В противном случае мы принимаем гипотезу Н₁. Это означает, что при заданном уровне значимости в уравнении регрессии присутствует систематическая ошибка, и это уравнение должно быть уточнено.

Проверка гипотезы о том, что дисперсия ошибки постоянна Упорядочим исходную выборку (x_k,y_k), k = 1,...,N по возрастанию величины x. Обозначим как N_1/2 половину от объема выборки, то есть N_1/2 = ЦЕЛОЕ (N /2). Выберем число M < N_1/2. После этого по упорядоченной по возрастанию величины x выборке рассчитаем отклонения от линии регрессии, первое для k = 1,...,M (для меньших значений x), второе для k = N — M +1,...,N (для больших значений x). Для лучшего разграничения между двумя группами наблюдений число М можно выбрать таким образом, чтобы исключить до 20% серединных точек.

В случае постоянства дисперсии ошибок МНК необъясненная дисперсия для меньших значений x должна быть приблизительно равна необъясненной дисперсии для больших значений x , то есть должно быть справедливым следующее равенство:

M N

Z *2 - Z *2

k=1 k=N —M+1

Обозначим большую из этих сумм как S1 , а меньшую как S2 .

Чем ближе к единице отношение S₁² / S2, тем больше оснований рассчитывать на то, что дисперсия ошибок МНК постоянна. Случайная величина F = S₁² / S2 подчиняется F -распределению Фишера с ?₁ = M — 2, ?₂ = M — 2 степенями свободы. Проверка гипотезы о постоянстве дисперсии ошибок осуществляется по следующей схеме:

q = 0.05 или q = 0.01

3) Критерий проверки

F = Si

S 2

4) Правило принятия решения

1—q, v1, v2

Принять Н₀, если F < F₁

В противном случае принять Н_і , то есть Н_і принимается, когда критерий проверки F попадает в критическую об^{ласть F} > ^Fi — q,_vi,_v2-

5) Проверка гипотезы

- Если F < F_{1—q v1 v2}, то критерий проверки F не попадает в

критическую область и мы принимаем гипотезу Н₀. Это означает, что при заданном уровне значимости дисперсия ошибок уравнения регрессии постоянна.

- В противном случае мы принимаем гипотезу Ні . Это означает, что при заданном уровне значимости уравнении регрессии не является наилучшим приближением исходных данных.

Непостоянство дисперсии ошибок МНК возникает как правило в том случае, если неправильно выбран вид математической модели зависимости фактора Х и отклика Y. Например, если нелинейную зависимость пытаются аппроксимировать линейной функцией.

Проверка гипотезы о том, что ошибки независимы

Одним из предполагаемых свойств уравнения регрессии y = ax + b + e является то, что ошибки е независимы между

собой. На практике проверяется не независимость, а некоррелированность этих величин, которая является необходимым, но недостаточным признаком независимости. При этом проверяется некоррелированность не любых, а соседних величин ошибок, которые можно получить, если исходная выборка (x_k,y_k)k = 1,...,N упорядочена по возрастанию величины х.

Рассмотрим например корреляцию ошибок, сдвинутых друг относительно друга на один шаг.

126

^е1 ^e2 ^e3 ••• ^ek ¦¦¦ ^eN

^е1 ^e2 ••• ^ek-1 ••• ^eN-1 ^eN

Тогда значение выборочного коэффициента корреляции между выборкой (e₂,e₃,...,e_N) и выборкой (e₁,e₂,...,e_N-1) запишется в

виде:

N-1

S ^(ek^{- e)(e}k+1

k=1_

e)

Pk ,k+1

N-1

N-1
S(ek - e)2 k=1		e)

Эту величину называют еще коэффициентом автокорреляции первого порядка. Так как согласно допущениям МНК математическое ожидание ошибки равно нулю, то формулу можно упростить:

N-1

S ^ek^ek+1

^pk ,k+1

k=1

N-1
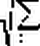
2 k		e 2 k+1

N-1
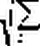
	e

Мы можем считать, что автокорреляция отсутствует, если выборочный коэффициент автокорреляции незначимо отличается от нуля, то есть в данном случае мы должны проверить гипотезу:

^H 0 ^{: p}k ,k+1 <sup>0

H</sup>1 : ^pk ,k+1 * ⁰

В случае однофакторной линейной регрессии случайная

^Pk ,k+1

будет подчиняться

величина

,k+1

^{1 -}Pk

распределению Стьюдента с V = (N -1) - 2 степенями свободы. Поэтому гипотеза будет проверяться следующим образом:

1) Гипотеза

^H 0 ^{: p}k ,k+1 = <sup>0

H</sup>1^: Pk ,k+1 * ⁰

127

2) Принятая величина уровня значимости q = 0.05 или q = 0.01

3) Критерий проверки

Pk ,k+1

^{1 p}k ,k+1

4)

5)

Правило принятия решения

Принтъ ^Н0, ^{если - t}1-q/2, ? < ^t < ^t1-q/2,?

В противном случае принять Ні , то есть Ні принимается, когда критерий проверки t попадает в критическую область

I ^t I > ^t1-q/2, ? ¦

Проверка гипотезы

Если - t_{1-q /2 ?} < t < t_{1-q /2 ?}, то критерий проверки t не попадает в критическую область и мы принимаем гипотезу Н₀. Это означает, что при заданном уровне значимости выборочный коэффициент автокорреляции первого порядка

Pk к+₁ статистически незначимо отличается от нуля. Следовательно, автокорреляция первого порядка ошибок МНК отсутствует.

В противном случае мы принимаем гипотезу Н_і. Это может означать, что нужно принять другую аналитическую модель зависимости между переменными Х и Y.

8.14. Сведение нелинейной функциональной зависимости к линейной путем преобразования данных.

До сих пор мы обсуждали линейную зависимость между фактором Х и откликом Y. Когда истинная взаимосвязь между ними носит нелинейный характер, в ряде случаев ее можно свести к линейной путем соответствующего преобразования данных. После этого к преобразованным данным может быть применена линейная регрессия. Преобразованные переменные и параметры мы будем отмечать символом п (например X).

В этом параграфе мы рассмотрим несколько наиболее употребительных видов нелинейной зависимости.

128

1) Экспоненциальная функция у = Ье^а

Экспоненциальная функция используется, когда при увеличении фактора Х отклик Y растет (а > 0) или снижается (а < 0) с постоянной относительной скоростью.

Приведение к линейной зависимости у = ах + b

осуществляется путем следующего преобразования данных: у = ln(y) X = х а = а b = ln(b)

2) Логарифмическая функция у = b + а ln(х)

Логарифмическая функция используется, когда при увеличении фактора Х отклик Y растет (а > 0) или снижается (а < 0) с уменьшающейся скоростью при отсутствии предельно возможного значения. Преобразование данных:

у = у X = ln( х) а = а b = b

3) Степенная функция у = bx°

Степенная функция используется когда при увеличении фактора Х отклик Y растет или снижается с разной мерой пропорциональности. Преобразование данных: у = 1п(у) X = ln(x) а = а b = ln(b)

4)

5)

Логистическая функция у =-:—г-—

^ s 1 + е (x-b)/а

Логистическая кривая имеет вид положенной на бок латинской буквы S. Она описывает случай когда при увеличении фактора Х отклик Y изменяется (снижается при а > 0 или растет при а < 0 ) в пределах от 0 до 1. При этом изменения происходят при х < b с увеличивающейся скоростью и при х > b с уменьшающейся скоростью. Преобразование данных:

у = ln(1 / у -1) х = х а = 1/а b =-b / а

Гиперболическая функция у = c +

129

Во многих случаях для аппроксимации нелинейной зависимости очень удобно использовать гиперболу, однако зачастую об этом трудно догадаться. Дело в том, что мы легко узнаем только простую гиперболу, асимптотами которой являются оси координат, то есть у = a / x . Если эта гипербола сдвинута вдоль одной из осей или вдоль обеих осей, то ее как правило не узнают.

Проверка того, является ли данная кривая гиперболой со сдвигом только вдоль оси х, то есть y = a /(x + b), проводится путем следующего преобразования данных: у = 1/y x = x a = 1/a b = b / a Проверка того, является ли данная кривая гиперболой со сдвигом только вдоль оси у, то есть у = c + a / x, проводится путем преобразования данных: у = у x = 1/x a = a b = c

Особенно сложным является случай, когда гипербола сдвинута одновременно по обеим осям, то есть имеет вид a

у = c +--. В этом случае нужно двигаться методом по-

x+b

следовательных приближений, то есть

- задавать ряд значений параметра b,

- вычислять значения 1 /(x + b) ,

- строить графики, где по оси абсцисс откладывать 1 /(x + b) , по оси ординат у,

- выбрать то значение параметра b, при котором график наиболее близок к прямой линии.

8.15. Функция регрессии как комбинация нескольких функций.

На практике может оказаться, что функцию регрессии невозможно описать удовлетворительным образом ни линейной зависимостью, ни любой из перечисленных в предыдущем параграфе нелинейных функций. Тогда стоит попытаться аппроксимировать ее комбинацией этих функций. Делается это следующим образом:

130

- В общем случае считаем, что зависимость между фактором Х и откликом Y нелинейна. Тогда, используя результаты из предыдущего параграфа, преобразуем исходную выборку (^хк,Ук),к = 1,...,N таким образом, чтобы в первом приближении можно было считать, что связь между преобразованными данными (Х_к,у_к),к = 1,...,N носит линейный характер.

- Вычисляем параметры линейной регрессии.

- Вычисляем ошибки МНК е_к, к = 1,..., N .

- Проверяем свойства ошибок МНК. Если ошибки не удовлетворяют допущениям МНК, то полученная аппроксимация является слишком грубой.

- Дальнейшее уточнение модели можно сделать, если в качестве зависимой переменной использовать полученные ошибки, то есть выборка приобретает вид (Х_к, е_к ), к = 1,..., N. Эту выборку необходимо обработать по

той же схеме. Процесс продолжается до тех пор, пока на определенном шаге ошибки не станут удовлетворять допущениям МНК. При этом надо помнить, что нельзя излишне переусложнять модель, и что полученные по модели результаты должны разумным образом интерпретироваться.



Содержание раздела

---