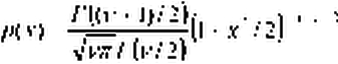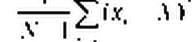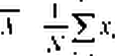Специальные распределения вероятностей

3.1. t-распределение Стьюдента.

Плотность распределения Стьюдента описывается формулой:


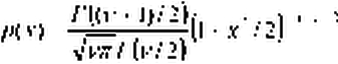
- да < х < +да

Распределение имеет вид колоколообразной кривой, симметричной относительно точки t = 0, и зависит от единственного параметра V, который принято называть числом степеней свободы. Приведем значения основных характеристик распределения Стьюдента:

Математическое ожидание, медиана, мода

Дисперсия

0 при V > 1

при V > 2

V-2

Коэффициент асимметрии Эксцесс

3(v- 2) (V- 4)

при V > 4

При числе степеней свободы V ^ да, распределение Стьюдента стремится к стандартному нормальному распределению, то есть к нормальному распределению с центром 0 и дисперсией 1.

Типичная интерпретация

1) Пусть случайная величина Х имеет нормальное распределение

„ 2

с математическим ожиданием /и и дисперсией 7 .

Если имеется выборка этой случайной величины (х₁, х₂X_N ), то состоятельными и несмещенными оценками

математического ожидания и дисперсии по выборке будут следующие величины:

-2 1 N
7

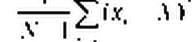
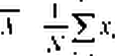
подчиняться распределению Стьюдента с V = N — 1 степенями свободы.

2)

Пусть случайные величины Х и Y имеют нормальное распределение с математическими ожиданиями и дисперсиями

⁽?х ^,0Х⁾ и (v_y->Оу) соответственно.

Если имеются выборки этих случайных величин (Хі, Х2,..., Xn ) и (Уі, y 2yN ), то состоятельной и несмещенной оценкой коэффициента корреляции между этими величинами по выборке будет:

N

_ Z⁽x^—X ')⁽Ук<sup>— Y)

x</sup>k^—v _t X—? _б

—=— и t = =—Т= будут

о о Ы N

Тогда случайные величины t

к=1

р =-

Z (Хк — X )²

Z (Ук — Y )²

к=1

к=1

Тогда случайная величина t = ? N — 2 • , =¦ будет

подчиняться распределению Стьюдента с V = N — 2 степенями свободы.

Вычисление распределения Стьюдента с помощью Microsoft Excel

Приведем несколько примеров вычисления характеристик распределения Стьюдента. Все используемые функции можно найти в разделе "Статистические функции" электронных таблиц Microsoft Excel.

Пусть случайная величина X подчиняется распределению Стьюдента с числом степеней свободы V .

1) Вероятность того, что X < x :

1 — СТЬЮДРАСП ( х, ?,1)

2) Вероятность того, что X > x :

СТЬЮДРАСП ( х, ?,1)

54

3) Вероятность того, что — х < X < x , вычисляется как:

P = 1 — СТЬЮДРАСП (х, ?,2)

4) Вероятность того, что | X | > х , равна: q = СТЬЮДРАСП (х,?,2)

Величина q - это вероятность того, что случайная величина

X попадает в критическую область распределения Стьюдента.

5) Если известна вероятность q того, что | X | > х, то соответствующее значение х равно:

х = СТЬЮДРАСПОБР (q,v)

6) Если известна вероятность q того, что X > х, то соответствующее значение х равно:

х = СТЬЮДРАСПОБР(2q, ?)

3.2. х -распределение.

Плотность ^-распределения задается формулой: х < 0: р( х) = 0

х^{(? 2)/2} • exp(- х/2)

х > 0: р(х) =

Г (?/2)2

?/2

Плотность зависит от единственного параметра ?, который принято называть числом степеней свободы. Приведем значения основных характеристик распределения:

Математическое ожидание ?

Мода ? — 2 (? > 2)

Дисперсия 2?

Коэффициент асимметрии 2л/2І?

Эксцесс 3? +12

?

55

При числе степеней свободы ? ^ да, X-распределение стремится к нормальному распределению с центром ? и дисперсией 2?.

Типичная интерпретация

Пусть случайная величина Х имеет нормальное распределение с математическим ожиданием ц и дисперсией а².

Если имеется выборка этой случайной величины (Xj, x₂,..., x_N), то состоятельными и несмещенными оценками

математического ожидания и дисперсии по выборке будут следующие величины:

^а =—“Г I^(хк ^{- X)}

' ¹ к=1

N-

— 1 ^{N X} = ^ IX»

к=1

N

Тогда случайная величина X ²=I(( (к — ц)/а)² будет

к=1

подчиняться X-распределению с ? = N степенями свободы, а случайная величина X = (N — 1)• (а /а²) будет подчиняться X -распределению с ? = N — 1 степенями свободы.

Вычисление X-распределения с помощью Microsoft Excel

Приведем несколько примеров вычисления характеристик X²-распределения. Все используемые функции можно найти в разделе "Статистические функции" электронных таблиц Microsoft Excel.

Пусть случайная величина X подчиняется X-

распределению с числом степеней свободы ? .

1) Вероятность того, что X < х, вычисляется как:

P = 1 — ХИ 2РАСП (х, ?)

2) Вероятность того, что X > х, равна: q = ХИ 2 РАСП (х, ?)

Величина q - это вероятность того, что случайная величина X попадает в критическую область x²-распределения.

56

3) Если известна вероятность P или вероятность q, то соответствующее значение x, определяющее границу интервала X < x равно: x = ХИ2ОБР(q, ?) или x = ХИ2ОБР(1 - P, ?)

3.3. F-распределение (распределение v²).

Плотность ^-распределения задается формулой:

x < 0 : p(x) = 0

x > 0:

^Г (⁽Vi +v₂⁾/²)

Г (?2)Г (V2/2)

P^{( x)} = iyJ^v2 )"^l/2

x(ч ^2)/2 ,(i + (v₁/v₂) • x)

(Vi + v₂)il

Плотность ^-распределения зависит от двух параметров (?₁,?₂), которые принято называть числом степеней свободы. Приведем значения основных характеристик ^-распределения:

Математическое

ожидание

^?2

?₂ ^{- 2}

при ?₂ > 2

^?2^(?і ^{- 2)}

?і(?₂ + ²⁾

Мода

при ?₁ > 2

Дисперсия

²?₂²⁽?і +?₂ ^{- 2) ?}1^(?2 ^{- 2)2(?}2 ^{- 4)}

при ?₂ > 4

Типичная интерпретация

Пусть случайные величины Х и Y имеют нормальное

22

распределение с дисперсиями cr_x и и_y соответственно.

Если имеются выборки этих случайных величин (xi, x2,..., x_N) и (Уі, У2,..., Ум), то состоятельными и

несмещенными оценками дисперсий по выборке будут следующие величины:

57

21 о „ -¦

-У (х_к - X)²

у -1 кі ^у м-\,=

Пусть выборочная дисперсия величины Х больше выборочной дисперсии величины Y . Тогда случайная величина

F = о_х / о_y будет подчиняться F-распределению с

?₁ = N - 1, ?₂ = M -1 степенями свободы.

У (У, - Y )<sup>2

1</sup> к=1

⁰х =

Вычисление F-распределения с помощью Microsoft Excel

Приведем несколько примеров вычисления характеристик F-распределения. Все используемые функции можно найти в разделе "Статистические функции" электронных таблиц Microsoft Excel.

Пусть случайная величина X подчиняется F-распределению с числом степеней свободы ?₁, ?₂.

1) Вероятность того, что X < х, вычисляется как:

P = 1 - FPACn (х,?₁,?₂)

2) Вероятность того, что X > х, равна: q = FPACn (х, ?₁, ?₂)

Величина q - это вероятность того, что случайная величина X попадает в критическую область F-распределения.

3) Если известна вероятность P или вероятность q, то соответствующее значение х, определяющее границу интервала X < х равно:

х = FPACПОБP(q, ?₁, ?₂) или х = FPACПОБP(1 - P, ?₁, ?₂)



Содержание раздела

---