Аналитические законы распределения случайных величин

2.1. Введение.

В этой главе мы рассмотрим наиболее употребительные законы распределения случайных величин, а также основные параметры этих законов. Будут даны методы поиска функции распределения вероятности случайной величины в случае неинтегрируемой плотности вероятности, а также алгоритмы получения последовательностей случайных величин с произвольным законом распределения, что необходимо при моделировании случайных процессов. Особое внимание будет уделено обобщенному экспоненциальному распределению, которое наиболее пригодно при изучении ценообразования активов.

2.2. Биномиальное распределение.

Пусть некоторое событие может иметь только два исхода, которые назовем "успех" и "неудача", при этом вероятность успеха равна р , вероятность неудачи равна (1 — р).

Если проводится серия из N независимых испытаний, то вероятность того, что успех в данной серии повторится х раз, а неудача (N — х) раз, будет равна произведению числа способов, которыми можно выбрать x из N , на вероятность того, что сначала х раз повторится успех, а затем (N — х) раз повторится неудача.

Следовательно, вероятность х успехов в N независимых испытаниях равна:

N! _N

р( х) = _!( д/ р^х (1 — р)^N—х х = 0,1,..., N

х!( N — х),

Данная формула описывает биномиальный закон распределения случайной величины. Из формулы непосредственно следует, что биномиальный закон полностью характеризуется двумя параметрами: количеством испытаний N и вероятностью успеха р . На рисунке приведена плотность биномиального распределения при N = 10 и различных значениях вероятности успеха р . Распределение является дискретным, поэтому точки соединены на графике лишь для наглядности.



0.50 -|

01 23456789 10

0.45

0.40

0.35

0.30

0.25

0.20

0.15

0.10

0.05

0.00

Математическое ожидание и дисперсия биномиального распределения составляют: р = Np D = Np(1 - p)

Третий центральный момент данного распределения равен ^m3 = ^NP^{(1 -} Р^{)(1 - 2} Р⁾

Следовательно, коэффициент асимметрии составляет

1 - 2 р

Знак коэффициент асимметрии зависит от вероятности успеха р :

Y < 0, еслир > 0.5

Y = 0, если р = 0.5

Y > 0, еслир < 0.5

Если вероятность успеха р фиксирована, то коэффициент асимметрии Y М’ 0 при количестве испытаний N М ж для любой р . Четвертый центральный момент данного распределения равен т₄ = ^(1 - р)[1 + 3(N - 2)р(1 - р)]. Следовательно, эксцесс составляет

1 + 3(N - 2)р(1 - р) Л^^{1 -} р)

31

При количестве испытаний N ^ да эксцесс биномиального распределения стремится к числу три, то есть к эксцессу нормального распределения.

2.3. Распределение Пуассона.

Распределение Пуассона называют еще распределением редких событий. Ему подчиняются случайные величины, вероятность появления которых в отдельном испытании мала и постоянна.

Распределение Пуассона является предельным случаем биномиального распределения. Его можно применить, когда количество испытаний N достаточно велико, а вероятность успеха р мала,

но так что произведение р = Np - это некоторое конечное постоянное число.

Если мы обозначим математическое ожидание количества успехов за некоторый промежуток времени (или за некоторое количество испытаний) как р, то вероятность получить х успехов за этот промежуток времени подчиняется распределению Пуассона:

_e~^ри^х

Р⁽ х⁾ =-— ^х = 0,1,2,...

х!

Данное распределение зависит от единственного параметра р , который может принимать конечные положительные значения. Напомним, что величина х - это количество успехов, а потому дискретна.

Из формулы для распределения Пуассона непосредственно следует, что р( х +1)/ р( х) = р/( х +1). Если р< 1, то Р^{( х} +¹⁾ < р(х) при любом х и максимальное значение р(х) достигается при х = 0. Если же р > 1, то р(х) сначала растет с увеличением х, достигая максимума при х ~ р, а затем убывает. Математическое ожидание и дисперсия распределения Пуассона равны р .

Третий центральный момент т₃ также равен р. Следовательно, коэффициент асимметрии составляет Y = 1/ -^~р , то есть распределение Пуассона имеет положительную асимметрию. Асимметрия стремится к нулю при р ^ да.

32

Четвертый центральный момент т₄ = 3р² + Л . Следовательно, эксцесс составляет S = 3 +1/ /л. При л ^ ж эксцесс распределения Пуассона стремится к числу три, то есть к эксцессу нормального распределения.

На рисунке приведена плотность распределения Пуассона при различных значениях математического ожидания. Распределение является дискретным, поэтому точки соединены на графике лишь для наглядности.

0.50

01 23456789 10

2.4. Равномерное распределение.

Если все значения непрерывной случайной величины в некотором интервале от а до b, равновероятны, то аналитически это можно записать в виде: р(х) = 0 х < a, х > b

р(х) = 1/(b - а) а < х < b

Распределение с такой плотностью вероятности называется равномерным (равновероятным, прямоугольным). Данное распределение часто используют для качественного анализа статистических процессов.

Математическое ожидание и дисперсия равномерного распределения составляют:

Л = (а + b)/2 D = (b - а)²/12

33

Медиана распределения совпадает с математическим ожиданием, моды не существует.

Коэффициент асимметрии и эксцесс равны: у = 0, s = 1.8 .

Для равномерного распределения можно в явном виде найти функцию распределения вероятностей:

F (х) = 0 х < a

F (х) = (х - a)l(b - a) a < х < b

F (х) = 1 х > b

Встроенный в компьютер генератор псевдослучайных чисел выдает числа, равномерно распределенные в интервале от 0 до 1. С их помощью можно моделировать случайные процессы с произвольной функцией распределения. Подробнее о том, как это делается, будет рассказано далее в этой главе.

2.5. Нормальное распределение.

Одним из важнейших распределений, встречающихся в статистике, является нормальное распределение (распределение Гаусса), относящееся к классу экспоненциальных. Плотность вероятности этого распределения:

^{(х -}и)

2с²

Р^{( х)} =

-exp

- да < х < +да

?2пст

Распределение имеет вид симметричной колоколообразной кривой, распространяющейся по всей числовой оси. Распределение Гаусса зависит от двух параметров: (и, с).

Математическое ожидание, медиана и мода данного распределения равны /и, а дисперсия и². Кривая плотности вероятности симметрична относительно математического ожидания. Коэффициент асимметрии и эксцесс равны у = 0, s = 3 .

Часто плотность нормального распределения записывают не как функцию переменной х, а как функцию переменной z = (х — и) l с, которая имеет нулевое математическое ожидание и дисперсию, равную 1. Плотность вероятности при этом равна:

34


exp

?2П

Такое распределение называют стандартным нормальным распределением.

Плотность вероятности распределения Гаусса нельзя проинтегрировать для получения интегральной функции распределения вероятностей F(x) в явном виде. F(x) можно найти с использованием:

- численных методов интегрирования функции р(х),

- путем разложения функции р(х) в ряд с последующим аналитическим интегрированием этого ряда.

Широкое применение распределения Гаусса в статистике основано на доказанном в теории вероятностей утверждении, что случайная величина, являющаяся суммой большого числа независимых случайных величин с конечными дисперсиями и с практически произвольными законами распределения, распределена нормально.

То есть условием использования нормального распределения для описания случайной величины являются ситуации, когда изучаемую случайную величину можно представить в виде суммы достаточно большого количества независимых слагаемых, каждое из которых мало влияет на сумму.

Распределение Гаусса можно использовать в качестве первого приближения для описания, например, логарифмов относительного изменения цен активов. Однако, только в качестве первого приближения, потому что на практике распределения этих величин отличаются от нормального, то есть имеют как правило более ярко выраженный пик и более "тяжелые" хвосты. Следовательно эти распределения являются островершинными и имеют эксцесс, превышающий три (иногда очень существенно).

Вычисление нормального распределения с помощью Microsoft Excel

Приведем несколько примеров вычисления характеристик нормального распределения. Все используемые функции можно найти в разделе "Статистические функции" электронных таблиц Microsoft Excel.

35

Пусть случайная величина X подчиняется нормальному распределению с параметрами (ц, о).

1) Плотность распределения в точке X = x:

НОРМРАСП (х, ц, о, ложь)

2) Вероятность того, что X < x :

НОРМРАСП (х, ц, о, истина)

3) Вероятность того, что X > x :

1 — НОРМРАСП(х, ц, о, истина)

4) Если известна вероятность того, что X < x, то есть P = P{X < x}, то соответствующее значение x можно вычислить как:

x = НОРМОБР( P, ц,о)

5) Для приведения нормально распределенной случайной величины к стандартному виду, то есть для вычисления z = (x — ц)/ о используется функция:

z = НОРМАЛИЗАЦИЯ (х, ц, о)

Пусть случайная величина Z подчиняется стандартному нормальному распределению (ц = 0, о = 1).

1) Вероятность того, что Z < z :

НОРМСТРАСП ( z )

2) Вероятность того, что Z > z :

1 — НОРМСТРАСП (z)

3) Если известна вероятность того, что Z < z, то есть P = P{Z < z}, то соответствующее значение z можно вычислить как:

z = НОРМСГОБРЦ)

4) Вероятность того, что — z < Z < z :

НОРМСТРАСП (z) — НОРМСТРАСП (—z)

5) Если известна вероятность того, что — z < Z < z , то есть P = P{—z < Z < z}, то соответствующее значение z можно вычислить как:

z = НОРМСТОБР((1 + P)/ 2) или

36

z = -НОРМСГОБР((\ - P)/ 2)

2.6. Логнормальное распределение.

Пусть х - нормально распределенная случайная величина с плотностью распределения:

(х-?)

2ст²

Рх ^(х) =

- да < х < +да

¦exp

42жо

Тогда случайная величина у, связанная с величиной х соотношением у(х) = в^х будет распределена логнормально. Заметим, что у может принимать значения только от 0 до +да. Найдем основные параметры логнормального распределения.

Обозначим неизвестную пока плотность логнормального распределения через р_у (у), которую определим исходя из равенства дифференциалов:

Ру ⁽y)dy = Рх ^(x)dx ^ Ру ⁽у⁾ = Рх ^[х(У^)] •^{dx /} dy

Так как х(у) = 1п(у), и dx / dy = 1/ у, для плотности вероятности логнормального распределения получается следующая формула:

(1n(у) - Ц) 2ст²

exp V

Ру ⁽у ⁾

0 < у < +да

Параметры логнормального распределения выражаются через параметры соответствующего распределения Гаусса следующим образом:

Цу = ^ехр(ц+ст^2/2)

D_y = ехр(2ц + ст²) • (ехр(ст²) -1)

Me = ехр(ц)

Mo = ехр(ц-ст²)

Распределение имеет крутой левый и пологий правый спад, то есть имеет положительную асимметрию.

Как и в случае распределения Гаусса, плотность вероятности логнормального распределения нельзя проинтегрировать

37

для получения функции распределения вероятностей в явном виде.

Однако, значения интегральной функции логнормального распределения можно найти, используя значения интегральной функции распределения Гаусса, так как они связаны соотношением F_y (y) = F_x[ln(y)], или в явном виде:

y ^ln( У ⁾

j Py ^{(t )dt} = j Px ^(t )dt

0 -ад

Логнормальное распределение можно использовать в качестве первого приближения для описания относительного изменения цен активов, однако, с теми ограничениями, о которых было сказано при обсуждении распределения Гаусса.

2.7. Распределение Лапласа.

Еще одним типом экспоненциального распределения, наряду с нормальным, является распределение Лапласа, плотность которого выражается формулой:

^-Ц

P^{( х)} =

-ад < x < +ад

-exp

42с

'42

Как и распределение Гаусса, распределение Лапласа:

- зависит от двух параметров (ц, с),

- математическое ожидание, медиана и мода данного распределения равны /и, а дисперсия с²,

- кривая плотности вероятности симметрична относительно математического ожидания, коэффициент асимметрии равен нулю.

Однако эксцесс распределения s = 6, то есть вдвое превышает эксцесс нормального распределения. Следовательно, распределение Лапласа островершинное, то есть имеет высокий пик и "тяжелые" хвосты.

Кроме того, плотность данного распределения интегрируема, и функция распределения может быть получена в явном виде:

38

Г

I^х

о/л/2 ;

F (х) = 0.5 • exp

I^х

О/Л ;

Г

F (х) = 1 - 0.5 • exp

Распределение Лапласа можно использовать для описания логарифмов относительного изменения цен активов, зачастую с большим успехом, чем нормальное распределение. Однако, с еще большей точностью, реальные распределения вероятностей описывает обобщенное экспоненциальное распределение, которое будет также рассмотрено в этой главе.

2.8. Распределение Коши.

Распределение Коши является одним из простейших законов распределения. Его плотность выражается формулой:

Р^{( х)}

_1_

bn(1 + [(х - a)/b]²)

Плотность распределения Коши имеет вид симметричной относительно точки х = а кривой, визуально очень похожей на плотность нормального распределения.

Кроме того р(х) интегрируема, поэтому функцию распределения Коши можно записать в явном виде и не прибегать при ее вычислении к помощи численных методов:

F(х) = — +—arctg[(х - а) / b]

2 ж

Казалось бы, распределение Коши выглядит очень привлекательно для описания и моделирования случайных величин. Однако в действительности это не так. Свойства распределения Коши резко отличны от свойств распределения Гаусса, Лапласа и других экспоненциальных распределений.

Дело в том, что распределение Коши близко к предельно пологому. Напомним, что распределение называется предельно пологим, если при х ^ ±го его плотность вероятности

р(х) = 1/ | х |¹⁺⁵, где 5 - сколь угодно малое положительное

число. При более пологих, чем 1/| х |¹⁺⁵ спадах, площадь под

39

кривой бесконечна, то есть не выполняется условие нормирования, и такие кривые не могут описывать плотность распределения вероятностей.

Для распределения Коши не существует даже первого начального момента распределения, то есть математического ожидания, так как определяющий его интеграл расходится. При этом распределение имеет и медиану и моду, которые равны параметру a.

Разумеется, дисперсия этого распределения (второй центральный момент) также равна бесконечности. На практике это означает, что оценка дисперсии по выборке из распределения Коши будет неограниченно возрастать с увеличением объема данных.

Из вышесказанного следует, что аппроксимация распределением Коши случайных процессов, которые характеризуются конечным математическим ожиданием и конечной дисперсией, неправомерна.

2.9. Распределение Парето.

Распределение Парето - это усеченное слева распределение, плотность вероятности и функция распределения которого выражаются в виде:

х < B : p(x) = F(х) = 0

х > B > 0,а> 0: p(x) = — (BI x)^l+a F(x) = 1 — (B/x)^a

B

Плотность р(х) распределения равна нулю при x < B, имеет максимальное значение при x = B и монотонно убывает при x > B .

Распределение Парето можно модифицировать таким образом, чтобы его можно было использовать для описания симметричных распределений вероятностей.

Введя новую переменную t = x — B, получим

p(t)=a. [ b /(b+1)]-=а. [i/(i+1 / B)f

B B

0 < t < +ro, B > 0, a > 0

Взяв величину t по модулю, эту формулу можно распространить на всю числовую ось, введя при этом нормировочный коэффициент 1/2.

40

P(t) = 2- • [1/(1+111 / Б)]"-

2Б

- да < t < Б > 0, a > 0

Описываемое последней формулой распределение имеет центр в точке t = 0. Для распределения с центром в произвольной точке t = A получим _a

P(t) = — • [1/(1+11 - A | / B)T^a

2 Б

-да < t < +да, Б > 0, a > 0

Итак, мы получили симметричное распределение, зависящее от трех параметров, с помощью которого можно описывать выборки случайных величин, в том числе с пологими спадами. Однако, это распределение обладает недостатками, которые были рассмотрены при обсуждении распределения Коши, а именно, математическое ожидание существует только при a > 1, дисперсия конечна только при a > 2, и вообще, конечный момент распределения к-го порядка существует при a > k .

2.10. Обобщенное экспоненциальное распределение.

Выше в этой главе были рассмотрены два вида экспоненциальных распределений: Гаусса и Лапласа. У них много общего: они симметричны, зависят от двух параметров (у, ст), имеют конечные моменты любого порядка. Отличие же состоит в том, что из-за того, что переменная х возводится в разную степень под знаком экспоненты (в квадрат у распределения Гаусса и в первую степень у распределения Лапласа), эксцесс у них разный. Напомним, что эксцесс характеризует остроту пика распределения и крутизну спада хвостов распределения. Возникает вопрос: можно ли записать формулу для плотности вероятности экспоненциального распределения в общем виде, то есть с произвольной положительной степенью переменной х под знаком экспоненты? Оказывается, такая формула существует:

exp	f x-у a Л V Act )

a

2 Г (1/ a) Act

Р^{( х)}

- да < x < +да

41

A = j Г (На) Г (3/а)

где Г(t) - это гамма-функция. О том, как вычисляется гамма-функция, рассказано в ПРИЛОЖЕНИИ 2.1 к этой главе.

Распределение с приведенной выше плотностью вероятности мы будем называть обобщенным экспоненциальным распределением, которое характеризуется тремя параметрами:

- математическим ожиданием (медианой, модой) ^,

- среднеквадратичным отклонением о (дисперсией о²),

- показателем степени распределения а .

Показатель степени а характеризует форму распределения:

- при а < 1 распределение имеет очень острый пик и очень пологие спады,

- при а = 1 распределение тождественно распределению

Лапласа,

- при а = 2 распределение тождественно распределению

Гаусса,

- при а > 2 распределение становится похожим на

равнобедренную трапецию, то есть имеет плоскую вершину и резко спадающие хвосты,

- при а ^ ж распределение тождественно равномерному

распределению.

Эксцесс распределения однозначно определяется показателем степени a: s = Г(1 /а)Г(5/а)/[Г(3/а)]².

Соответственно, из вычисленного по выборке случайных величин значения оценки эксцесса, можно определить оценку показателя

а .

Обычно в справочниках распределения Гаусса, Лапласа и равномерное рассматриваются как разные распределения, хотя в излагаемой здесь концепции - это одно и тоже распределение. Единственным параметром, характеризующим форму (а значит и свойства) этих распределений является показатель а .

В дальнейшем, если принята гипотеза о том, что плотность вероятности случайной величины имеет экспоненциальный характер, для описания этой величины будем использовать именно обобщенное экспоненциальное распределение.

На рисунке приведена плотность стандартного обобщенного экспоненциального распределения при различных значениях а .

42


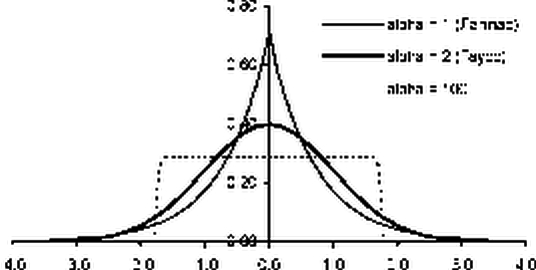
В общем случае плотность вероятности обобщенного экспоненциального распределения нельзя проинтегрировать для получения функции распределения вероятностей F(x) в явном виде. F(x) можно найти с использованием:

- численных методов интегрирования функции р(х),

- путем разложения функции р(х) в ряд с последующим аналитическим интегрированием этого ряда.

О том, как это делается, будет рассказано в следующих параграфах.

Вычисление интегральной функции обобщенного экспоненциального распределения в Microsoft Excel

Не приводя доказательства скажем, что интегральная функция обобщенного экспоненциального распределения может быть выражена через интегральную функцию гамма-распределения (встроенная функция Excel) следующим образом:

1

, —,1, ИСТИНА а

x >!і: F(x) = 0.5 + 0.5 • ГАММАРАСП

Х<7

1

, —,1, ИСТИНА а

x - и Хи

F(x) = 0.5 - 0.5 • ГАММАРАСП

x < /и :

2.11. Поиск интегральной функции распределения путем численного интегрирования плотности распределения.

Пусть дана случайная величина, которая подчиняется обобщенному экспоненциальному распределению с параметрами

43

(^,G,a) , то есть плотность вероятности имеет вид:

exp	f x — ^ а Л V Ли )

Р^{( x)} =

a

— Ж <x< +Ж

2 Г (1/а) Лег

Требуется найти интегральную функцию распределения: F (x) = I p( z )dz

Прежде всего заметим, что задачу можно упростить, перейдя к переменной t = (x — fj.) / G. Случайная величина t имеет математи

ческое ожидание, равное нулю, и дисперсию, равную единице. Формулы для плотности вероятности и функции распределения примут вид:

exp(—I t/ Л|^а)

a

2 Г (1/а)Л

P^(t)

— ж < t < +Ж

t

^{F (t)} = I p^{( z )dz}

Для решения поставленной задачи достаточно:

- разбить всю область определения переменной t на N интервалов, при этом узлы разбиения будут образовывать массив

T }, k = 0,..., N.

- вычислить в узлах разбиения массив значений интегральной функции {F_k }, k = 0,..., N.

Тогда для произвольного значения переменной t, такого, что T_k < t < T_k+1 значение интегральной функции F(t) может быть приближенно определено в виде:

F (t) = F_k + (t — T_k )(Fk+\ — F_k ) l(T_k+i — T_k )

Так как между узлами разбиения величина F аппроксимируется линейной зависимостью, то интервал разбиения должен быть достаточно мал, то есть количество узлов разбиения достаточно велико.

Однако, плотность вероятности определена на всей числовой оси, а разбить бесконечный интервал на конечное количество интервалов конечной длины невозможно. Поэтому приближенно будем считать, что

44

p(t) =-—-exp(-11/ ЛЯ")

2 Г (II а) Я ^{v 1} ' ¹⁷

p(t) = 0 111 > R

^{F (t)} = { P^{( z )dz}

- R

где величину 2R назовем размахом распределения.

Очевидно, интервал от - R до R можно трактовать как интерквантильный промежуток с некоторой близкой к единице доверительной вероятностью. Для обобщенного

экспоненциального распределения половину размаха можно задать эмпирически полученной формулой:

R = ?3 + 4.788 • (е-1.8)²¹³

После введения понятия размаха распределения, все готово для написания алгоритма решения задачи:

1) Задаем входные данные: показатель степени распределения а и количество интервалов разбиения N (целое четное число).

2) Вычисляем эксцесс распределения

е = Г (1I а) Г (51 а) І[ Г (31 а)]²

3) Вычисляем половину размаха распределения R = 43 + 4.788 • (е-1.8)²¹³

4) Вычисляем минимальное и максимальное значение переменной t

-R

T_m

R

5)

6) 7)

Вычисляем массив узлов на оси t T_k = T_min + (T_max - T_mm)k IN k = 0,..., N

Вычисляем номер центра распределения

M = N12

Вычисляем массив значений плотности вероятности для k от 0 до М

(-1TJ А^а)

k = 1,...,M

Pk =

exp

2 Г (1Іа)Я

Po = ⁰

45

8) Вычисляем вспомогательный массив, в котором величины p_k суммируются нарастающим итогом для k от 0 до М

^Sk =Z Pi ^k = ^0,->^M

i=0

9) Так как значение интегральной функции в центре распределения (то есть в узле с номером М) равно 0.5, то можно вычислить левую часть массива, в котором содержится функция распределения

Fk = 0.5• Sk /Sm k = 0,...,M

10) Так как распределение симметрично относительно центра, вычисляем оставшуюся часть массива, в котором содержится функция распределения

^Fk = ^{1 - F}N-k ^k = ^M + ^1,..._> ^N

Итак, мы получили массив значений случайной величины {T_k} и соответствующий ему массив интегральной функции распределения {F_k}, то есть задали функцию распределения в табличном виде.

Для произвольного значения переменной t значение интегральной функции F(t) может быть определено по формулам:

t < T₀: F (t) = 0

^Tk <^t < ^Tk+i ^k = ⁰v-^{N -1:}

F(t) = F_k + (t - Tk )(Fk+1 - Fk )/(7k₊1 - T_k ) t > T_N : F (t) = 1

Напомним, что переменная t имеет нулевое математическое ожидание и единичную дисперсию. Переменная х с произвольными математическим ожиданием и дисперсией связана с переменной t соотношением x = p + ot.

2.12. Поиск интегральной функции распределения путем разложения плотности распределения в ряд с последующим аналитическим интегрированием этого ряда.

Задачу, поставленную в предыдущем параграфе, можно решить путем разложения стоящей под знаком интеграла функции в ряд Тейлора с последующим интегрированием этого

46

ряда. Итак, нам нужно проинтегрировать обобщенное экспоненциальное распределение (р = 0, о = 1) :

exp(-| t/Ар)

a

2 Г (1 ta)X

Pit⁾

- ш < t < +ш

t

^{F (t)} = j P^{( z} )dz

Так как плотность распределения симметрична относительно центра, для нахождения интегральной функции распределения достаточно вычислить

j exp(- (z / Xf f

і

q^(t) = j P^{( z})dz

2 Г (1/a)X

- jexp(-(z / Xff (z / X)

I J ^{V /}

j exp⁽- y^a)d}

t/X

^{2 Г (1/a)}0 ^{2 Г (1/a)} 0

Функцию под знаком интеграла можно разложить в ряд Тейлора следующим образом:

^ш Л

exp(- y-fT (-1) ‘У-

k=0 ^k!

Подставив это разложение под знак интеграла и проведя интегрирование, получим

ak+1

q^(t) = ¦

i-1)‘ (t / X)

2 Г (1/a) k=0 k! ak +1

Практически, суммирование производится не до да, а до некоторого k=N, такого, что

_! (t/X)^a+¹ <₈ N!' aN +1 <

где 8 - это некоторое наперед заданное малое положительное число (точность вычисления). То есть мы должны вычислить частичную сумму ряда.

Функция распределения F (t) связана с q(t) соотношениями: t > 0: F(t) = 0.5 + q(t) t < 0: F(t) = 0.5 - q(| 11)

47

2.13. Моделирование с помощью равномерного распределения случайных чисел с произвольной плотностью распределения.

Встроенный в компьютер генератор псевдослучайных чисел выдает числа, равномерно распределенные в интервале от 0 до 1. Так как любая интегральная функция распределения F(x) имеет область значений от 0 до 1, то с помощью равномерного распределения можно получить случайное число с произвольным законом распределения путем решения обратной задачи, то есть восстанавливая по известному значению F(x) значение х. В качестве примера будем моделировать случайную величину, подчиняющуюся обобщенному экспоненциальному

распределению. Для решения этой задачи будем использовать результаты, полученные в двух предыдущих параграфах.

Постановка задачи

Дано случайное число z, равномерно распределенное на интервале от 0 до 1.

Требуется получить число x, подчиняющееся обобщенному экспоненциальному распределению, с параметрами (p,G,a) .

Решение путем предварительного численного интегрирования плотности распределения, то есть задания функции распределения в табличном виде.

Для получения искомого числа х, найдем сначала вспомогательное число t, которое подчиняется обобщенному экспоненциальному распределению, с параметрами (р = 0, G = 1) .

Для этого по методике, изложенной в параграфе 2.11, получим массив значений случайной величины {T_k} и соответствующий

ему массив интегральной функции распределения {F_k}, то есть

зададим функцию распределения в табличном виде. Для произвольного значения переменной t значение интегральной функции F(t) может быть определено как: t < T₀: F (t) = 0

Tk < t < Tk+1 k = 0,..., N -1:

F (t) = Fk + (t - T_h)(F_k+1 - F_h) /(Tk+1 - T_h) t > Tn : F (t) = 1

48

На интервале Т₀ < t < T_N величины t и F связаны линейно.

Если принять, что величина t не может быть меньше Т₀ и не может быть больше T_N , то можно получить обратную зависимость t (F) в виде:

F = 0: t(F) = Т F = 1: t(F) = Tn

^Fk < ^F < ^Fk+i ^k = ^0,•••^,N-1:

t(F) = T_k + (F - F_k )(T_k+l - T_k )/(F_k+1 - F_k )

Если считать, что полученная с помощью генератора случайных чисел величина z является значением функции распределения F в некоторой точке t, то величина t может быть найдена по приведенным выше формулам, где вместо переменной F подставлена величина z. Искомое число х вычисляется как х = ju + at.

Решение методом итераций, с использованием вычисления функции распределения через ряд Тейлора.

Как и в предыдущем случае, для получения искомого числа х, найдем сначала вспомогательное число t, которое подчиняется обобщенному экспоненциальному распределению, с параметрами (U = 0,a = 1).

В параграфе 2.12 было показано, что можно вычислить функцию распределения F(t) в точке t с требуемой точностью как частичную сумму соответствующего ряда. Теперь нам нужно решить обратную задачу, то есть по известному значению F(t) найти неизвестное значение t. Точнее, в соответствии с условиями поставленной задачи, мы должны решить относительно t уравнение

F (t) - z = 0.

Для численного решения этого уравнения мы используем метод деления пополам. Для того, чтобы приступить к решению этим методом, необходимо задать конечный интервал, в котором должен лежать корень уравнения. В качестве области возможных значений t выберем интервал от -R до R, где 2R - это рассмотренный выше размах распределения. Считаем, что F(-R) = 0, F(R) = 1.

Численное решение уравнения F(t) - z = 0 с заданной точностью означает, что достаточно найти такое t, при котором

49

z <5, где S - это некоторое наперед заданное малое поло

|F (t)

жительное число (точность вычисления).

Решение состоит в последовательном повторении шагов (итераций), до тех пор, пока не будет достигнута необходимая точность:

1) Задаем начальные величины граничных значений переменных t и F

T

m

T_m

-R Fm R F_m

2)

3)

4)

5)

6)

Вычисляем текущее значение t как среднее значение между Tmin

^{и T}max ^t - ^(Tmin + ^Tmax^{)/ 2}

Вычисляем по методике из параграфа 2.12 величину F(t) Проверяем условие | F — z| <5. Если неравенство

справедливо, то необходимая точность решения достигнута и текущее значение t является решением.

В случае F — z >5 изменяем значения величин T_min, T_max,

^Fmin, ^Fmax-

- если F < z, то

T _{— t} F _— F

min min

T , F_max остаются без изменения

IIldA ¹ IIldA

- если F > z, то

T_min, F_min остаются без изменения

T _{— t} F _— F

max ’ max

Возвращаемся на шаг 2.

После того, как необходимая точность вычисления величины t достигнута, искомое число x находится как x — /и + Gt. На практике чаще всего необходимо получить не отдельное случайное число x с заданным законом распределения, а последовательность таких чисел {x_k }, k — 0,...,N. Это необходимо, как правило, при моделировании случайных процессов. В этом случае описанные в данном параграфе процедуры нужно повторить соответствующее количество раз.

50

ПРИЛОЖЕНИЕ 2.1. Гамма-функция Эйлера.

Гамма-функция, обобщающая понятие факториала, является одной из важнейших специальных функций. Для произвольного положительного х, значение Г(х) задается формулой:

Г(х) = I e~^tt^x~¹dt х > 0

0

В этом приложении мы рассмотрим алгоритм вычисления гамма-функции. Данный алгоритм основан на следующем ее свойстве: Г(х +1) = х ¦ Г(х) для любого х > 0. Это свойство позволяет свести вычисление Г(х) от любого х к вычислению гамма-функции на интервале 1 < х < 2, на котором ее можно аппроксимировать полиномом пятой степени:

Г (х) = a₀ + a₁ х + a₂ х² + a₃ х³ + a ₄ х ⁴ + a₅ х⁵

a₀ = 3.69764701987851

a₁ = -6.60156185480728

a₂ = 6.37763107208549

a₃ = -3.26329362313704

a₄ = 0.885309940132118

a₅ = -0.0957403771932692

Область значений величины х > 0 можно разбить на три интервала, на каждом из которых Г (х) вычисляется следующим образом:

1) 1 < х < 2

В этом случае, Г(х) непосредственно вычисляется с помощью приведенного выше полинома.

2) 0 < х < 1

В этом случае, Г(х) = Г(х +1) / х, и так как 1 < х +1 < 2, то Г (х +1) вычисляется с помощью полинома.

3) х > 2

В этом случае величину х можно представить в виде х = N + z, где

51

N - это целая часть x (N > 2), z - это дробная часть x (0 < z < 1).

Тогда

Г(х) = Г(N + z) = (N + z -1)Г(N + z -1) = ... =

N-i

= Г(1 + z)n (N + z - k)

k=1

и так как 1 < z +1 < 2, то Г(z +1) вычисляется с помощью полинома.

Вычисление гамма-функции с помощью Microsoft Excel

В Microsoft Excel гамма-функцию можно вычислить, используя следующую комбинацию функций:

Г ( х) = ЕХР( ГАММАНЛОГ ( х))



Содержание раздела

---