Вероятностное описание случайных величин
1.1. Введение.
Теория вероятностей играет значительную роль во многих областях человеческой деятельности, в том числе в финансах. Это связано с тем, что результаты решения об инвестировании в финансовые инструменты (активы) всегда имеют ту или иную степень неопределенности.
В биржевых торгах по различным активам принимают участие большое количество инвесторов и спекулянтов. Каждый из участников имеет свое представление о том, куда движется рынок, у каждого из них свой горизонт инвестирования и своя технология работы на рынке. Из-за столкновения интересов большого количества людей цены активов приобретают случайный характер. Следствием этого является невозможность точного предсказания будущей цены. Прогноз становится возможным только в вероятностном смысле.
С другой стороны, результаты инвестирования в инструменты с фиксированной доходностью также являются неопределенными из-за того, что существует риск невыполнения эмитентом (заемщиком) своих обязательств.
В этой главе мы рассмотрим на качественном уровне понятие вероятности, случайного события, случайной величины, дадим определение закона распределения случайной величины. Далее будут изучены основные параметры законов распределения, такие как показатели центра распределения, показатели меры рассеяния, показатели формы распределения.
1.2. Случайное событие. Вероятность.
Случайным событием называется такое событие, которое может как произойти, так и не произойти при соблюдении определенного комплекса условий. Будем предполагать, что указанный комплекс условий может быть воспроизведен неограниченное количество раз. Испытанием будем называть каждое осуществление этого комплекса условий.
Относительной частотой случайного события называется отношение количества случаев появления этого события M к общему числу проведенных испытаний N.
Опыт показывает, что при многократном повторении испытаний относительная частота M/N случайного события обладает устойчивостью. В разных достаточно длинных сериях испытаний относительные частоты случайного события группируются вокруг некоторого определенного числа. Устойчивость относительной частоты может быть объяснена как проявление объективного свойства случайного события, которое заключается в существовании определенной степени его возможности.
Таким образом, степень возможности случайного события можно описать числом. Это число называется вероятностью случайного события. Именно вокруг вероятности группируются относительные частоты данного случайного события. Относительная частота и вероятность случайного события являются безразмерными величинами, которые могут принимать значения от 0 до 1. Вероятность является первичным, базовым понятием, и в общем случае ее нельзя определить через более простые термины.
1.3. Случайная величина.
Случайной величиной называется такая величина, которая принимает те или иные значения с определенными вероятностями. Случайные величины могут быть дискретными и непрерывными.
Дискретной случайной величиной называется такая величина, все возможные значения которой образуют конечную или бесконечную последовательность чисел (x
1, x
2,..., x
n) и
принятие ей каждого из указанных значений есть случайное событие, характеризующееся соответствующей вероятностью (p
1, p
2,..., p
n). При этом должно соблюдаться условие нормирования, то есть ^ p
n = 1.
n
Непрерывной случайной величиной называется такая величина, все возможные значения которой целиком заполняют некоторый промежуток и попадание в любой интервал (x
1, x
2)
14
есть случайное событие, характеризующееся соответствующей вероятностью P{x
1 < x < x
2}. При этом вероятность достоверного события Р{—го < x < +го} = 1.
Генеральной совокупностью будем называть все возможные значения, которые может принимать случайная величина.
1.4. Законы распределения случайной величины.
Для характеристики вероятности появления различных значений случайной величины используют законы распределения вероятностей случайной величины. При этом различают два вида представления законов распределения: интегральный и
дифференцальный.
Интегральным законом, или функцией распределения вероятностей случайной величины X, называется функция, значение которой для любого x является вероятностью события, заключающегося в том, что случайная величина X принимает значения, меньшие x, то есть функция F(x) = P{X < x}. Функция распределения вероятностей F (x) обладает следующими свойствами:
1) 0 < F(x) < 1 для любого x
2) F (xi) < F (x
2), если x1 < x2
3) F (-го) = 0, F (+ro) = 1
Для случайной величины с непрерывной и дифференцируемой функцией распределения вероятностей F (x) можно найти дифференциальный закон распределения вероятностей, выражаемый как производная F(x), то есть p(x) = dF(x)/ dx. Эта зависимость называется плотностью распределения вероятностей. Плотность распределения p( x) обладает следующими свойствами:
1) p(x) > 0 для любого x
x
2) Р{X < x} = F(x) = I p(t)dt
—ro
b
3) P{a < X < b} = F(b) — F(a) = |p(t)dt
a
15
+ад
4) I p( x)dx = 1
—ад
Распределение называется предельно пологим, если при x ^ его плотность вероятности p(x) = 1/| x |
1+5 , где 5 -сколь угодно малое положительное число. При более пологих, чем 1/ | x |
1+5 спадах, площадь под кривой бесконечна, то есть не выполняется условие нормирования, и такие кривые не могут описывать плотность распределения вероятностей.
1.5. Показатели центра распределения.
Координата центра распределения определяет положение случайной величины на числовой оси. Дать однозначное определение этого понятия невозможно. Центр распределения может быть найден несколькими способами:
- как медиана распределения,
- как мода распределения,
- как математическое ожидание.
Медиана
Наиболее общим, а следовательно наиболее фундаментальным, является определение центра распределения согласно принципу симметрии, то есть как такой точки на оси x, слева и справа от которой вероятности появления случайной величины одинаковы и равны 0.5. Такой показатель центра распределения называется медианой. В отличие от других показателей центра, медиана существует у любого распределения. Медиану обычно обозначают как Me .
Мода
Точка на оси x, соответствующая максимуму кривой плотности распределения, называется модой, то есть мода - это наиболее вероятное значение случайной величины. Однако, мода существует не у всех распределений. В качестве примера можно привести равномерное распределение. В этом случае определение центра распределение как моды невозможно. Моду обычно обозначают как Mo .
16
Математическое ожидание
Наиболее часто используемым методом оценки центра распределения является математическое ожидание. Преимущественное использование математического ожидания объясняется тем, что это единственная оценка, которую можно выразить аналитически.
Математическое ожидание обозначается как /и и вычисляется по формулам:
- для дискретного распределения
М (х) = Ц = ^
хпр
п
п
- для непрерывного распределения
+ад
М (х) = ц = j xp( x)dx
—ад
Необходимо отметить, что математическое ожидание существует только у тех распределений, у которых при х ^ ±ад
плотность вероятности спадает как 1/| х|
2+5 или круче, где 5 -сколь угодно малое положительное число. При более пологих, чем 1/| х |
2+
5 спадах, математическое ожидание не существует, так как определяющий его интеграл расходится.
1.6. Моменты распределения.
Для описания свойств распределений нам понадобится понятие момента распределения. Существуют два типа моментов: начальные и центральные. Начальным называется момент распределения, найденный без исключения систематической составляющей. Соответственно, центральным является момент, вычисленный с исключением систематической составляющей. Начальный момент k-го порядка вычисляется по формулам:
- для дискретного распределения
Мк = ?
хІРп
n
- для непрерывного распределения
+ад
М
к = j х
к p( x)dx
—ад
17
Первый начальный момент был уже рассмотрен выше - это математическое ожидание.
Центральный момент k-го порядка вычисляется по формулам:
- для дискретного распределения
mk =Z
(xn -MfPn
n
- для непрерывного распределения
+ад
m
k = I (x - fSf p( x)dx
— ад
Понятие моментов распределения будет использовано при изучении показателей рассеяния случайной величины и показателей формы распределения.
1.7. Показатели меры рассеяния.
Оценив величину центра распределения, нам необходимо иметь представление, как случайная величина рассеяна вокруг этой точки. Для оценки меры рассеяния используются, как правило, два способа:
- квантильное отклонение случайной величины,
- дисперсия и среднеквадратичное отклонение случайной величины.
Квантильное отклонение
Площадь, заключенная под кривой плотности распределения p(x), согласно правилу нормирования, равна единице, то есть отражает вероятность всех возможных событий.
Выберем точку Хі на оси х таким образом, чтобы площадь под кривой р(х) слева от точки Х
і была бы равна, например, 5% от общей площади, то есть вероятность того, что случайная величина меньше, чем Х
і составляет 0.05. В этом случае говорят, что Х
і - это 5%-ная квантиль распределения. Ее удобно обозначить как
X1 = X 0.05.
Выберем далее точку Х
3 на оси х таким образом, чтобы площадь под кривой р(х) слева от точки Х
3 была бы равна 95% от общей площади, то есть вероятность того, что случайная величина
18
меньше, чем Х
3 составляет 0.95. Тогда Х
3 - это 95%-ная квантиль распределения. Обозначим ее как X
3 = Х
0 95.
Медиана распределения - это 50%-ная квантиль, так как она делит площадь под кривой р(х) на две равные части. Медиану можно обозначить как X
2 = X
0 50.
Заметим, что точки X
1 = X
0 05 и X
3 = Х
0 95 симметричны в том смысле, что
- во-первых, вероятность того, что случайная величина меньше Хі, и вероятность того, что случайная величина больше Х
3, равны между собой,
- во-вторых, вероятность того, что случайная величина находится в интервале от Х
і до Х
2, и вероятность того, что случайная величина находится в интервале от Х
2 до Х
3, также равны между собой.
Интервал значений х между X
1 = X
0 05 и X
3 = X
0 95 называют интерквантильным промежутком с 90%-ной вероятностью. Его протяженность А
0 90 = X
0 95 — X
005. Половину указанного промежутка, которую будем называть квантильным отклонением с 90%-ной вероятностью, обозначим как d
0 90 = А
0 90 / 2 .
На основании вышеизложенного подхода можно ввести понятие квантильной оценки рассеяния случайной величины, то есть значения рассеяния с заданной доверительной вероятностью. Для симметричных распределений квантильное рассеяние с заданной доверительной вероятностью P - это такой интервал неопределенности (X
0 50 — d
p, X
0 50 + d
p ), внутри которого лежат 100P процентов всех значений случайной величины, а 100(1 — P)
процентов лежат вне этого интервала.
Так как квантили, ограничивающие доверительный интервал, могут быть различными, при указании квантильной оценки рассеяния обязательно должна быть указана доверительная вероятность такой оценки. Квантильная оценка рассеяния применима для любых законов распределения случайной величины.
При рассмотрении квантильного отклонения, мы не случайно в качестве примера использовали отклонение с 90%-ной доверительной вероятностью. Дело в том, что величина d
0 90 обладает уникальным свойством, которое заключается в том, что только
19
квантильное отклонение d
0 90 имеет однозначное соотношение со среднеквадратичным отклонением ст (которое будет рассмотрено ниже) в виде d
090 ~ 1.6ст для очень широкого класса наиболее
употребительных законов распределения. Поэтому, при отсутствии данных о виде закона распределения, для оценки квантильного отклонения рекомендуется пользоваться доверительной вероятностью, равной 0.90.
Дисперсия и среднеквадратичное отклонение
Если в качестве показателя центра распределения выбрано математическое ожидание, то в качестве меры рассеяния случайной величины используют дисперсию. Дисперсия - это среднее значение квадратов отклонений случайной величины от ее математического ожидания. Дисперсия является вторым центральным моментом распределения.
Дисперсия обозначается как D и вычисляется по формулам:
- для дискретного распределения
D = Z
(xn
—и
)2 Pn
n
- для непрерывного распределения
+ад
D = I(x - /и)
2 p(x)dx
—ад
В формуле для дисперсии в качестве центра распределения использовано математическое ожидание. Это не случайно. Дело в том, что использование в качестве центра распределения математического ожидания минимизирует средний квадрат отклонения случайной величины от ее центра. При этом минимум среднего квадрата отклонений как раз и равен дисперсии. Дисперсия и математическое ожидание связаны соотношением:
D( x) = M (x
2) — [M (x)]
2
Дисперсия имеет размерность квадрата случайной величины. Поэтому для более наглядной характеристики рассеяния используют корень квадратный из дисперсии, который называется
среднеквадратичным отклонением (с.к.о.): ст = ^JD.
20
Дисперсия - наиболее широко применяемая оценка рассеяния случайных величин. Это связано с тем, что она обладает свойством аддитивности, то есть дисперсия суммы статистически независимых случайных величин равна сумме дисперсий этих величин, безотносительно к разнообразию законов распределения каждой из суммируемых величин и возможной деформации законов распределения при суммировании. Отметим, что среднеквадратичное отклонение не аддитивно.
Таким образом, для того, чтобы рассеяния случайных величин можно было суммировать аналитически, эти рассеяния должны быть представлены своими дисперсиями, а не кван-тильными (доверительными) отклонениями.
Однако, конечная дисперсия существует только у тех распределений, у которых при x ^ ±го плотность вероятности
спадает как 1/| x |
3+
5 или круче, где 5 - сколь угодно малое положительное число. При более пологих, чем 1/ | x |
3+
5 спадах, определяющий дисперсию интеграл расходится.
1.8. Показатели формы распределения - коэффициент асимметрии.
При изучении формы распределения случайной величины важно выяснить, симметрична ли относительно центра распределения кривая плотности вероятности. Показателем степени несимметричности этой кривой является безразмерная величина, называемая коэффициентом асимметрии. Коэффициент асимметрии обозначается как у или As. Рассмотрим на качественном уровне понятие асимметрии.
В случае, если кривая плотности вероятности имеет крутой левый и пологий правый спад, говорят, что распределение имеет положительную асимметрию. В этом случае координаты показателей центра распределения располагаются на оси абсцисс, как правило, следующим образом: мода < медиана < математическое ожидание.
Если кривая плотности вероятности имеет пологий левый и крутой правый спад, распределение имеет отрицательную асимметрию. В этом случае для показателей центра распределения имеем:
математическое ожидание < медиана < мода.
21
Наконец, у симметричных распределений, медиана, мода и математическое ожидание совпадают.
Разумеется, все вышесказанное о соотношении показателей центра, справедливо только для тех распределений, у которых существует мода и/или математическое ожидание. Напомним, что понятие медианы применимо к любому распределению.
Существует несколько методов для оценки коэффициента асимметрии.
Оценка коэффициента асимметрии с помощью квантилей распределения
Рассмотрим, например, интерквантильный промежуток с 90%-ной вероятностью. Напомним, что он образован с помощью 5%-ной и 95%-ной квантилей распределения. Тогда соответствующий коэффициент асимметрии вычисляется по следующей формуле:
( X 0.95 Xo.50 )
- (X 0.50 Xo.05
)
;
- 2X0
X0
X0
X0.95
X0.05
X0.95
X0.05
Разумеется, таким способом можно вычислить коэффициент асимметрии на любом интерквантильном промежутке, однако следует сказать, что подобная оценка будет зависеть от выбора интер-квантильного промежутка, то есть, например, оценка на 90%-ном и на 50%-ном промежутках будут давать вообще говоря разные результаты. Достоинством данного метода является то, что с его помощью можно рассчитать коэффициент асимметрии для любого распределения.
Оценка коэффициента асимметрии с помощью третьего центрального момента распределения
Если в качестве показателя центра распределения выбрано математическое ожидание, то коэффициент асимметрии рассчитывают, используя третий центральный момент распределения.
В этом случае коэффициент асимметрии - это отношение третьего центрального момента (имеющего размерность куба случайной величины) к среднеквадратичному отклонению (размерность которого совпадает с размерностью случайной величины), возведенному в третью степень.
Коэффициент асимметрии вычисляется по формулам:
- для дискретного распределения
22
Е (Xn -^)3 Pn
n_
для непрерывного распределения
+W
I(x - /и) p(x)dx
1.9. Показатели формы распределения - эксцесс.
Чрезвычайно важным показателем формы распределения является безразмерный показатель, называемый эксцессом. Эксцесс обозначается как s или Ex. Эксцесс характеризует:
- во-первых, остроту пика распределения,
- во-вторых, крутизну спада хвостов распределения.
Если за точку отсчета принять нормальное распределение (которое будет подробно рассмотрено ниже), то распределения плотности вероятности можно условно разделить на три группы:
- островершинные,
- средневершинные,
- плосковершинные.
Островершинные распределения характеризуются более выраженным, чем у нормального распределения, пиком и полого спадающими, "тяжелыми" хвостами.
Средневершинные распределения незначительно отличаются от нормального.
Плосковершинные распределения имеют слабо выраженный пик или совсем не имеют пика и, соответственно, моды. Кроме того, они характеризуются резко спадающими хвостами.
Определим эксцесс как отношение четвертого центрального момента распределения к среднеквадратичному отклонению, возведенному в четвертую степень. Эксцесс вычисляется по формулам:
- для дискретного распределения
Е
(xn
-U
)4 Pn
для непрерывного распределения
23
+ад
I (х - р( x)dx —ад
Для различных законов распределения эксцесс может иметь значение от 1 до +оо. Нормальное распределение имеет эксцесс, равный трем.
Эксцесс удобно использовать для характеристики остроты пика и крутизны спадов хвостов распределения:
- островершинные распределения имеют эксцесс > 3,
- средневершинные распределения имеют эксцесс « 3,
- плосковершинные распределения имеют эксцесс < 3,
Часто в качестве эксцесса используют отношение четвертого центрального момента к четвертой степени среднеквадратичного отклонения, за вычетом числа три. Однако здесь и далее мы будем рассчитывать эксцесс по приведенным выше формулам.
1.10. Плотность распределения функции от случайной величины.
Пусть Х - это случайная величина, имеющая плотность распределения р
х (х) . Найдем плотность распределения p
y (у)
случайной величины Y, которая является функцией от Х.
Пусть функция у(х) монотонно возрастает. Тогда любой интервал (х
1,х
2) взаимно однозначно отображается на интервал (У
1,У
2) ¦ Следовательно, вероятности попадания случайных величин Хи Y в соответствующие интервалы равны. В применении к малым интервалам это означает равенство дифференциалов вероятности:
Рх
(x)dx = Ру
(y
)dy
. .
г . dx Следовательно р
у (у) = р
х [ х( у)] • —
dy
где х(у) - это функция, обратная функции у(х).
Если функция у(х) монотонно убывает, то положительному значению dx соответствует отрицательное значение dy.
24
Следовательно, в уравнении равенства дифференциалов нужно
заменить dy на -dy=
dy\. Это приводит к более общей зависимости:
dx
dy
Ру
(У
) = Рх
[x(У )] •
Для иллюстрации вышесказанного рассмотрим несколько примеров.
1) у(х) = ax + b, a Ф 0
В зависимости от знака параметра a эта функция может быть как монотонно возрастающей, так и монотонно убывающей. Переменные х и у определены на всей числовой оси.
х( У
)
dx _ 1 dy a
Py
(y
) = p- Px ( J
I a | ^ a J
y( x) = x
3
Эта функция является монотонно возрастающей. Переменные х и y определены на всей числовой оси.
1/3 dx 1
x(y
) = y -
2)
2/3
dy 3y
Py
(y
) = -ф/3 Px
(y
1/3)
3)
y( x) = ln( x)
Эта функция является монотонно возрастающей. Переменная х определена на интервале от 0 до +». Переменная y определена на всей числовой оси.
x(y
) = e
y
— = e dy
Py
(y
) =
ePx
(e )
4) y( x) = e
- x
Эта функция является монотонно убывающей. Переменная х определена на всей числовой оси. Переменная y определена на интервале от 0 до +<».
25
dx 1
dy у
х( у
) =
- 1п( у) = 1п(1/ у
)
Ру
(У
) = -Рх
(п(1/У)) У >
0
у
Ру
(у
) =
0 у ^
0
у( х) = х
2
5)
Эта функция монотонно убывает на интервале от -со до 0 и монотонно возрастает на интервале от 0 до +о. Переменная х определена на всей числовой оси. Переменная у определена на интервале от 0 до +о.
dx _ 1
d =
- іу
71
х < 0: х(у) = -у
1'
2
х > 0: х(у) = у
1/2
1/2
ау 2 у
1
Следовательно
Рх (-у
1/2) +
Рх (у
1/2)
Ру
(у
) =
у>0
1/2 х
1/2 х
2у
Ру
(у
) =
0 у <
0
1.11. Математическое ожидание функции от случайной величины.
Математическое ожидание случайной величины Y, которая является функцией случайной величины Х, может быть вычислено без нахождения плотности вероятности этой функции, то есть непосредственно по распределению случайной величины Х.
Если обозначить математическое ожидание случайной величины Y как р
у, то справедливы следующие формулы:
- для дискретного распределения
Ру =
M[у
(х)] = Z у
(хп
)Рп
п
- для непрерывного распределения
26
+W
My =
M [ y
( x)] = j y
( x) P
( x)dx
Заметим, что в общем случае /л
у * y
(Mx )•
1.12. Линейное преобразование случайной величины.
В дальнейшем наиболее часто мы будем использовать линейное преобразование случайной величины, то есть преобразование вида y(x) = ax + b. В этом случае параметры
распределения величин Х и Y связаны соотношениями: My =
aMx +
b Dy = a
2 • Dx
Vy = I
a I
Vx
Одним из важнейших примеров линейного преобразования является преобразование случайной величины к стандартному виду (нормирование):
x-Mx
t = t (x)
То есть случайная величина х с произвольным математическим ожиданием и произвольной дисперсией преобразуется в случайную величину t с нулевым математическим ожиданием и единичной дисперсией и среднеквадратичным отклонением. Величина t называется стандартизованной (нормированной) случайной величиной.
1.13. Общие свойства случайных величин с произвольным законом распределения.
Независимо от закона распределения случайной величины существуют общие свойства распределений вероятностей. К ним можно отнести:
- неравенства, определяющие граничные значения вероятности попадания случайной величины в заданный интервал,
- законы больших чисел, определяющие свойства достаточно большого количества случайных величин.
27
Неравенство Чебышева
Неравенство Чебышева определяет граничное значение вероятности попадания случайной величины x с произвольным законом распределения, имеющей математическое ожидание и
2
и дисперсию о , в заданный интервал вокруг математического ожидания:
Р{|
x-и\>
Ло} <Л Р{|
x - и\-
Ло} > 1
-jf
Иными словами, вероятность того, что в некотором испытании случайная величина x окажется за пределами интервала, длина которого прямо пропорциональна с.к.о., убывает обратно пропорционально квадрату коэффициента пропорциональности Л.
Неравенство Чебышева определяет важность среднеквадратичного отклонения как характеристики рассеяния случайной величины относительно центра распределения.
Подставив в неравенство Чебышева несколько конкретных значений величины Л , получим, что для любых законов распределения с математическим ожиданием и и дисперсией
о
2 справедливо:
Л = 1: Р{| x-и\>о} < 1 Р{| x-и\<о} > 0
Л = 2: Р{| x — и | > 2о} < 1/4 Р{| x-и|< 2о} > 3/4
Л = 3: Р{| x - и | > 3о} < 1/9 Р{| x-и|< 3о} > 8/9
Законы больших чисел
Невозможно предвидеть, какое значение примет случайная величина в результате отдельного испытания. Однако, при достаточно большом количестве испытаний оценки по выборке параметров распределения случайных величин в достаточной степени утрачивают случайный характер. То же самое можно сказать и в отношении суммы большого количества случайных величин. При увеличении числа слагаемых колебания отдельных величин взаимно сглаживаются и закон распределения суммы приближается к нормальному
28
распределению. Различные утверждения, относящиеся к этим предельным случаям носят названия законов больших чисел.
Теорема Бернулли
Если в последовательности из N независимых испытаний вероятность p некоторого случайного события остается постоянной, то вероятность того, что отклонение эмпирической частоты этого события M / N от p не превзойдет заранее заданное число 8 > 0 стремится к единице:

Теорема Чебышева
Вероятность того, что отклонение среднего арифметического N независимых случайных величин с конечными дисперсиями от среднего арифметического их математических ожиданий не превзойдет заранее заданное число 8 > 0 стремится к единице
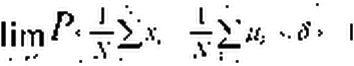
Из теоремы Чебышева следует, что с увеличением числа N среднее арифметическое случайных величин постепенно утрачивает характер случайной величины и все более стремится к константе.
Центральная предельная теорема (теорема Ляпунова)
Распределение суммы N независимых случайных величин с конечными дисперсиями и с произвольными законами распределения стремится к нормальному распределению при N ^ ж , если вклад отдельных слагаемых в сумму мал.
Теорема Ляпунова объясняет широкое распространение нормального закона распределения тем, что рассеяние случайных величин вызывается множеством случайных факторов, влияние каждого из которых ничтожно мало.
Содержание раздела