Б. Н. Нефедов - Дифференциальная аппроксимация динамических биржевых данных

Введение.
Вопросы, связанные с аппроксимацией функции, возникают в различных областях естествознания. Наиболее полное свое развитие получила теория аппроксимации функции по набору других, базисных, функций, получившая название "функционального анализа" и врядли нуждающаяся в литературных ссылках.

Источником функционального анализа являются начально-краевые задачи математической физики. Логическая цепочка здесь такова. Сперва формулируются общие законы, по которым развивается физический или иной процесс в пространстве и времени. Дифференциальная форма записи этих законов представляет собой начально-краевую задачу. Если доказана теорема о существовании и единственности ее решения, то можно перейти к его нахожденю. Одним из методов нахождения решения может быть функциональная аппроксимация. В наиболее простых случаях это разделение переменных и использование в качестве базисных функций множества решений обыкновенной однопараметрической краевой задачи типа Штурма-Лиувилля. Именно в этом направлении можно получить хоть какие-то точные решения для изучаемого процесса. В более сложных случаях, когда разделение переменных провести не удается, в качестве базисной системы функций может быть использованны решения более простой, решаемой, краевой задачи. Такой подход реализовывается в методе Галеркина.

Если же мы изучаем некий процесс на практике, то для нахождения общих законов, лежащих в основе его описания, нам требуется, как минимум, понятие опыта (лабораторного эксперимента), то есть возможность воспроизведения результатов наблюдения при неизменных внешних условиях. Именно этого во многих реальных процессах нам и не дано. Мы не можем повторить процесс, сохранив при этом внешние условия неизменными (т.е. изменение условий эксперимента и степень их воздествия на изучаемый процесс нельзя считать малыми величинами). Особенно ярко это проявляется в экономических процессах, где, как правило, имеется лишь одна временная реализация процесса и эксперементаль-ного воспроизведения она не допускает. Следовательно, мы не можем сформулировать динамическую начально-краевую задачу по единственному ее решению. Мы даже не можем определить размерность задачи, так как наблюдению и измерению, как правило, доступны далеко не все зависимые переменные.

Функциональная аппроксимация является всего лишь алгоритмом приближенного описания процесса. Сама по себе она не вскрывает его сути, законов его порождения. К одному и тому же процессу можно применить бесконечное множество функциональных аппроксимаций с разными базисами. Чаще, однако, встречается ситуация, когда функциональную аппрксимацию с одним и тем же базисом применяют к совершенно разнохарактерным процессам. Как правило, это тригонометрическое разложение Фурье (спектральный анализ), и является одним из частных случаев метода Галеркина, когда конкретизируется базисная система функций. Но если в (ограниченных) пространственных и периодических временных процессах данный подход работает эффективно (доказывается полнота и сепарабельность тригонометрической системы функций), то для временных непериодических процессов спектор тригонометрического разложения Фурье становится непрерывным и, если быть полным формалистом, его нельзя определить по конечному отрезку функции.

В данной работе предлагается другой подход к понятию аппроксимации. Вместо разложения по базисной системе функций мы будем строить линейную дифференциальную задачу Коши с постоянными коэффициентами (для временных процессов) по единственной доступной нам реализации процесса (грубо говоря, по одной кривой). Задача Коши

включает в себя обыкновенное дифференциальное уравнение порядка n, которое содержит в себе в качестве постоянных коэффициентов не менее n свободных параметров (некоторые из них можно заведомо положить равными нулю) и начальные значения зависимой переменной и ее производных до порядка (n-1) включительно, что также является параметрами аппроксимации. Таким образом, задача Коши n-ого порядка содержит не менее 2n свободных параметров, подлежащих определению.

Дифференциальное уравнение является следствием неких законов сохранения. Следовательно, для конкретного эксперементального процесса мы постулируем законы сохранения путем фиксации конкретного вида дифференциального уравнения задачи Коши и определим такой алгоритм подбора ее свободных параметров, чтобы наша эксперемен-тальная кривая "наилучшим" образом согласовывалась (аппроксимировалась) ее решением. Такой подход будем называть дифференциальной аппроксимацией эксперементальных данных или, коротко, дифференциальной аппроксимацией. Однако прежде чем приступить к формулировке и решению этой задачи, нам следует разобраться, с какими по своему характеру процессами мы можем столкнуться при реализации дифференциальной аппроксимации.

Стохастические и детерминированные процессы. Сформулируем необходимые определения. Прежде всего, мы считаем время непрерывной величиной. Тогда динамический процесс называется континуальным, если он определены в каждый момент времени. В теории передачи сигналов такие процессы назвают аналоговыми.

Под детерминированным континуальным процессом, или просто детерминированным процессом, будем понимать процесс, для которого в каждой точке его определения существуют лево- и правосторонние производные. Если же эти производные равны друг другу, то процесс является непрерывный в данной точке.

Под стохастическим континуальным процессом, или просто стохастическим процессом, будем понимать процесс, который не имеет производной в каждой точке своего существования. Другими словами, стохастический процесс почти в каждой точке своего существования испытывает скачек конечной величины и тем самым для каждой точки его существования невозможно определить даже односторонней предельно малой окрестности (е-окрестности), для того, чтобы существовал предел приращения AX/At при At^0 (нельзя устремить ДХ^0 при е^0).

Примером стохастического процесса служит процесс биржевого ценообразования. Напомним, что на бирже (или в обменном пункте валюты, если так нагляднее) для каждого эмитента в каждый момент времени имеется две цены -покупки и продажи. Разность между этими ценами всегда конечна и называется маржой. Мгновенной биржевой ценой эмитента, так уж сложилось исторически, называется цена той сделки, которая прошла в данный момент времени, причем неважно, какая именно сделка была совершена - покупка или продажа. Если теперь предполажить, что в каждый момент времени совершается сделка (континуальный процесс), то даже при постоянных ценах покупки и продажи и при условии, что этих сделок на каждом временном интервале совершается примерно одинаковое количество (условие стационарности), мы получим скачкообразный (стационарный стохастический) процесс изменения мгновенной цены биржевого эмитента. Именно из-за того, что в качестве цены фиксируется цена каждой сделки, на любом бесконечно малом интервале времени имеется бесконечно много (мощности континуума) скачков конечного размаха.

Несмотря на то, что понятие дифференцирования для стохастического процесса не существует, тем не менее, обратное понятие интегрирования, охватывающее как детерминированные, так и стохастические процессы, можно ввести, используя понятие интеграла Лебега. Точнее сказать, понятие интегрируемости по Лебегу было специально введено именно для подобных процессов. По Лебегу вся область определения функции разбивается на конечное количество непересекающихся интервалов (мер) и подсчитывается количество аргументов, при которых функция попадает в эту меру.

Затем количество длины интервалов разбиения устремляют к нулю, к количество отсчетов - к бесконечности. В дальнейшем все интегралы мы будем понимать в смысле Лебега.

Ответ на вопрос, какого рода динамический процесс изучается в данном конкретном случае на эксперименте - детерминированный или стохастический, далеко не очевиден. Связано это прежде всего с тем, что экспериментальные данные даже для континуальных процессов измеряются дискретным образом, как правило через равные (эквидистантные - равноотстоящие) промежутки времени. В результате эксперимента мы получаем дискретный набор данных. В разных разделах математики такие наборы называют по разному: сеточная функция, временной ряд, табличная функция. Все эти названия - синонимы.

Интереснее то, что мы всегда можем проинтерполировать эти дискретные данные гладкой функцией (и даже имеющей гладкую производную - это хорошо известная спайн-интерполяция). Получив гладкую интерполяцию, утверждать после этого, что исходный процесс носит стохастический характер, вообще говоря, становиться неудобным. Поэтому характер экспериментального процесса приходится определять исходя не из внешнего вида его дискретного представления, а из более детального, пусть даже качественного анализа, подобного проведенному выше для определения стохастического характера биржевого процесса.

С вычислительной точки зрения различия между интегрированием по Лебегу и по Риману не существует. Дело все в той же дискретности представления экспериментальных данных. Численное вычисление интегралов базируется именно на дискретном представлении, а площади вычисляемых фигур (по крайней мере, по формулам прямоугольников и трапеций) в обоих случаях одинаковы.

Введем понятие энергии континуального процесса X(t) на временном интервале te [to,t₁] ^t1

(1а)

^(ti ^to⁾

(1б)

I dtX²(t),

^t0 и скалярного произведения двух процессов на том же интервале

1 ^Х1

(X1,X2) = -----1dtX1(t)X2(t).

^(t1 ^t0⁾t₀

Для стохастических процессов (1а) представляет собой (выборочную) дисперсию (меру разброса), а (1б) -(выборочную) ковариацию (меру зависимости). Вместо ковариации обычно вводят понятие корреляции двух процессов, нормируя ковариацию

t

_х= (^X1^{, Х}2 ) ^e1^e2

| dtX1(t)X2(t)

*0

*1 t!

I dtX2(t) I dtX2(t)

^t0 ^t0

Считается, что процессы независимы, если %=0, то есть, если они ортогональны.

Для детерминированных процессов (1а) представляет собой норму, а (16) - скалярное произведение в гильбертовом пространстве L₂[t₀,t₁]. Правда, если более внимательно взглянуть на определение гильбертова пространства L₂, то можно просто включить стохастические континуальные процессы в множество элементов этого пространства. Часто L₂ называют энергетической метрикой, подчеркивая тот факт, что если X(t) представляет собой механистическую траекторию материальной точки, то X²(t) с точностью до постоянного множителя представляет собой ее потенциальную энергию.

Таким образом, вне зависимости от того, является ли процесс стохастическим или детерминированным, он характеризуется (с точностью до терминологии) одними и теми же интегральными характеристиками. Именно эти интегральные характеристики важны в теории аппроксимации, как функциональной, так и дифференциальной. Поэтому при аппроксимационном описании нет необходимости делать различия между стохастическими и детерминированными, и в дальнейшем будем говорить именно об энергии, а не о дисперсии или метрике, подчеркивая тем самым общность в аппроксимации континуальных процессов.

Постановка и решение задачи.

Запишем линейную задачу Коши n-ого порядка с постоянными коэффициентами

.(n-1)

r(n-2)

x⁽ⁿ⁾ + a_n-1x^{(n 1} + a_n-2 x^{(n 2)} +... + a₂x"+a₁ x'+a₀x = 0, x = x(t),

(2)

Xn-1).

^x(t0⁾ = ^x0^,x'^(t0⁾ = ^x1^,x"^(t0⁾ = ^x2^, ••• ^{,x(n 2)(t}0⁾ = ^xn-2^,x" ¹4^t0⁾ = ^xn-1-

Ключевой элемент дифференциальной аппроксимации состоит в том, что мы сопоставляем определенную на конечном интервале te [t₀,t₁] эксперементальную функцию X₀(t)eL₂[t₀,t₁] самой старшей производной задачи Коши (2)

x⁽ⁿ⁾(t) = X₀(t)

Тогда производные нижележащих порядков выражаются через квадратуры от X(t) и начальные условия:

x^(n-l)(t) = I dT X0( T) + x^(n-l)(t₀), x^(n-2|(t) = I^dT(t - T)^X0(T) + x^(n-1|(^t0)^t + x^(n-2)(^t0)

x^(t) = (_n - I^{dT(t - T)n-1X}0^(t) +

^t0

^L^₍ +... + ^x"^(t0⁾^7 + ^x'^(t0^)t + ^x(t0⁾.

(n - 2)! 2!

_t^n-1 _t

^{(n -1)!}

+ x^(n-1)(tc)— + x⁽"^-2)(t0bⁱ

При этом используется формула дифференцирования интеграла с параметрически изменяющимися пределами интегрирования

X(p(t),t)^-f⁾

dt

d ^{q(t) q(t)} d d_q(_t)

- JdT X(t, T) = J dT-X(t, T) + X(q(t),t)-d-<sup>)

dt</sup> p(t) p(t) ^{dt dt}

и формула преобразования многократного интеграла в однократный t t t 1 t

J ^dT J ^dT ... J ^{dT X(T)} = ₍ J ^{dT (t - т)П}"^1x(t).

to -o -o ^{(n 1)!}-o

n

В результате такой переформулировки задача Коши (2) трансформируется в интегральное уравнение Вольтерра второго рода

^Xo^(t) + an-1J ^{dT X}o^{( T)} + an _ 2 J ^{dT (t - T)X}o^{( t)} +..

J ^{dT (t -T)n - 3X}o^{( t)} +

(n - 3)!-t

to

+ ₍ ^a12)! J^{dT(t - T)n-2X}o^(T) + ₍ ^a°_1)! J^{dT(t - T)n-1 X}o^(T) +

⁽ⁿ -^1)!-

(n - 2)! -

o

n-1

n-21

tt

+ C_{n 1}^-+ C_{n 2} —-+... + C₂ — + C₁t + C_o = o.

^n-1(n -1)! ^n-2 (n - 2)! ² 2! ^{1 o}

Запишем более компактно это выражение

^XO^(t) + ^an-A-1^(t) + ^an-2^?п-2^(t) + ••• + ^aO0O^(t) + ^Сп-1^{-П 1} + ^Сп-2^{-П 2} + ••• + ^CO = ^O> ⁽³⁾ применив сокращающие обозначения

^{- -} 1 ^-0_n-1^(t) = J^dTXo^(T), 0_n-2^(t) = J^dT(t-T)Xo^(T), ••• A^(t) J^dT(t-T)n-1Xo^(T),

-o -o ^{(n 1)!}-o

^Cn-1 = ^aO^x(n-1)(tO<sup>)

a</sup>1^{x(n 1)(t}o⁾ + ^ao^{x(n 2)(t}o⁾

'n-2

(4)

(n - 2)

(n-1)

^(t0⁾ + ... + a₂x" ^(t0⁾ + ^a1^x' ^(t0 ⁾ + ^a0^x(t0<sup>)

(t</sup>0⁾ + ^an - 2

^С0

= ^an-1

Выражение (3) представляет собой линейную аппроксимацию нашей экспериментальной функции по степенным функциям и функциям, образованным в результате ее последовательного интегрирования, а поскольку сама функция нам известна, то и любой интеграл от нее можно вычислить. Коэффициенты аппроксимации можно получить стандартным методом наименьших квадратов. Для этого требуется минимизировать функционал

^J(an-1, ••• , ^a0, ^Cn-1, ••• , ^C0 ⁾

= Jdt[x0^(t) + ^an-^_n-1^(t) + ^an-2^i-2^(t) + ••• + ^a0^^(t) + ^Cn-1^{tn 1} + ^Cn-2^{tn 2} + ••• + ^C0. • ^t0

Необходимым и достаточным условием существования этого функционала является принадлежность X₀(t) гильбертову пространству L₂[t^₀,t₁] • Действительно, если сама функция квадратично интегрируема на конечном интервале, то таким же свойством обладают и функции, образованные из неё путем интегрирования, а следовательно функционал J существует и конечен Дифференцируя его по свободным параметрам, получаем линейную систему

алгебраических уравнений, в результате решения которой определяем ao,•••,a_n-l,Co,•••,C_n-l• Затем, решая

ДИ)^ =

диагональную систему (4), определяем начальные значения x(^) = Х0, •••,X⁽ⁿ ^(^) = X_n-1

Тем самым

полностью определяются все свободные параметры линейной дифференциальной задачи Коши (2) по известной экспериментальной функции X₀(t)e L₂[t₀,t₁] и задачу дифференциальной аппроксимации считаем решенной

Точное равенство (3) достигается лишь в том исключительном случае, когда экспериментальная функция X₀(t) в точности равна n-ой производной решения полученной задачи Коши В этом случае функционал (5) достигает своего теоретически минимального значения равного нулю. В любом другом случае возникает новая функция X₁(t), представляющая собой остаток от аппроксимации

ⁿ¹ + ^Cn-2^{tn 2} + ••• + ^C0 ⁽⁶⁾

x⁽ⁿ⁾ + a_n-1x^{(n 1)} + a_n-2 x^{(n 2)} + ••• + a₂x”+a₁ x'+a₀x = X₁ (t), x⁽ⁿ⁾ (t) = X₀ (t)

0⁷ (n-2).

0

^x(t0⁾ = ^x0. ^x'^(t0⁾ = ^x1. ^x”^(t0⁾ = ^x2^, ••• ^,^4^t0⁾ = ^xn-2^{, x(n-1)(t}0⁾ = ^xn-T

(7)

Хорошо известно, что общее решение такой задачи представимо в виде:

t

(8)

x^(t) = ^а 0Ф 0^(t) + ^a191^(t) + ••• + ^а n Ф n^(t) + J ^K01^(t,^{T )X}1^{( T )dT}

где фo(t),CPi(t), ... ,ф_n(t) - фундаментальная система решений однородного уравнения, tti, ... ,tt_n -

постоянные интегрирования, K₀₁ (t,T) - функция Коши. Дифференцируя n раз это решение

(n)

d¹

^Xo^(t) = x^(n)(t) = ^aoP0^n)(t) + ^aiP^(n)(t) +... + ^anPn^n)(t) + dtcny j^K01⁽t^T)X1^(T)dT

(9)

V *0

получим выражение исходного процесса X₀(t) через остаточный процесс X₁(t). Отметим без доказательства, что (9) является решением интегрального уравнения (6) и наоборот. Т.е. (6) и (9) - это взаимообратные выражения. Основная ценность выражения (9) состоит в том, что оно представляет собой разложение исходного экспериментального (и возможно, стохастического) процесса X(t) на аналитическую составляющую, выраженную через систему фундаментальных решений однородного дифференциального уравнения и интеграл, включающий в себя остаточный (от аппроксимации) процесс X₁(t), содержащий в себя всю возможную стохастику.

После того, как получен остаточный процесс X₁(t), его, в свою очередь, тоже можно подвергнуть процедуре дифференциальной аппроксимации:

\

J

\

J

d⁽ⁿ⁾

j K12 (t, T )X 2 ( T )d T

V *0

X, (t) = р 0 V 0ⁿ⁾(t) + в 1V ⁽ⁿ⁾(t) + ... + в n v nⁿ⁾(t) +

(n)

dt

(n)

X_N(t) = p 0 ? 0ⁿ⁾(t)+e.e(ⁿ⁾(t)+...+p n ? ⁽nⁿ⁾(t)+

j ^KN,N+1 ^(t, ^T)XN+1 ^(T)dT

V *0

(n)

dt

Теоретически, так можно продолжать бесконечное количество раз. Однако в практическом плане это имеет смысл продолжать лишь до тех пор, пока выполняется естественное требование, состоящее в том, чтобы энергия остаточного процесса была меньше энергии исходного процесса

Мерой изменения энергии может служить отношение



В том случае, если s>1, а следовательно, выполняется условие (10), мы будем говорить о том, что дифференциальная аппроксимация является эффективной или сжимаемой, поскольку энергия (как мера разброса) выходного процесса в этом случае меньше энергии входного процесса. Однако возможны, и на практике достаточно часто встречаются случаи, когда s<1. Такие аппроксимации назовем неэффективными или разжимаемыми.

Выбрав интервал данных для аппроксимации (или, коротко, интервал аппроксимации) и конкретный вид задачи Коши, мы тем самым получаем однозначную дифференциальную аппроксимацию. Если в результате аппроксимация оказалась неэффективной, и она нас не устраивает, то исправить это можно лишь изменив интервал данных (сузив или расширив его) или выбрать другую задачу Коши.

Важным следствием разложения (9) является понятие аппроксимационной производной. Формально, ее можно вычислить, еще один раз продифференцировав (9):



\

1⁽t ^T)X1^(T)dT J

d⁽ⁿ⁺¹⁾

dt⁽ⁿ+¹⁾

Xo^,(t⁾=x⁽ⁿ⁺¹⁾⁽t)=Oo90^n+1)(t)+o₁9⁽ⁿ⁺¹⁾⁽t⁾+o_n9nⁿ⁺¹⁾⁽t⁾+

(11)

Для детерминированного процесса аппроксимационная производная совпадает с обычной производной. Для стохастического процесса, как было отмечено выше, производной X’(t) в обычном смысле не существует и выражение (11), по крайней мере, в регулярной своей части, может служить аналогом обычной производной. Это справедливо, если считать остаточный процесс X₁(t) пренебрежимо малым стохастическим возмущением типа белого шума, т.е. процессом с нулевым средним значением и пренебрежимо малой энергией e₁<<1.

Частный случай.

Для иллюстрации приведенной общей теории рассмотрим простую и практически важную частную проблему аппроксимации экспериментальных данных гармонической задачей Коши

x”(t) + |ix(t) = 0, x(t0) = Х0, x'(^) = X1, ДФ 0. (12)

В ней имеется три свободных параметра, подлежащих определению: Д , x 1 , x 0 . Сопоставим экспериментальный временной процесс X₀(t) старшей, в данном случае второй, производной и проведем интегрирование:

^x”^(t) = ^X0<sup>(t)

x</sup>'^(t) = j ^{dT X}0^{( T)} + ^x'^(t0⁾,

^t0

^x(t) = j ^{dT (t - t)X}0^(t) + ^x'^(t0^)t + ^x(t0⁾-

^t0

Это дает нам интегральное уравнение t

X0(t) + Д j dT (t-t)X0(t) + C1t + C0 = 0, C1 =^x'(t0), C0 = Mx(^). (13)

^0

Используем его для составления вариационной задачи

-I 2

ч

J(|!,Ci,Co) = J dt

X₀ (t)+ц J dx (t - t)X₀ (t) + c₁t + c

^ min.

(14)

Минимум этого функционала достигается при выполнении условий

= 0,

^dJ = {dt

^X0^(t) + Ц j^{dT(t - t)X}0^(t) + C1^t + C0

*0 _

X₀(t) + ц J dT (t - t)X₀(t) + c₁t + c

Эс

0 t0

dJ ^tf_dt d = j ^dt

^dc1 t0

= 0,

(15)

dJ

1

^dt

J dT (t - t)X₀ (t) X₀ (t) + ц JdT(t - t)X₀(t) + c₁t + c₀

= 0.

Они представляют собой симметричную систему трех линейных алгебраических уравнений относительно трех неизвестных - C),^, Ц :

^(t1 ^{- t}0^)c0 + 2^(t1 ^{- t}0^)c1 + ^а02^Ц + ^Ь0 = ⁰,

12-2 1 3 .3

2 ^(t1 ^t0^)c0 + 3 ^(t1 ^t0^)c1 + ^а12^Ц + ^b1 = ⁰,

^a20^C0 + ^a21^C1 + ^а22^Ц + ^b2 = ⁰,

(16)

с коэффициентами ^t1 ^t

a02=a20=j dtJdx(t -t)Xo(t), a12=a21=j dtt Jdr(t -t)Xo(t), a22=j dt j dr(t -t)Xo(t)

^t0 ^t0 ^t0 ^t0 ^t0 V^t0

Для решения этой системы нет необходимости привлекать численные методы, как в случае систем более высокого порядка. Можно сразу выписать ее аналитическое решение, воспользовавшись формулами Крамера

t1 (t

^t1 t

A_c A_c А_ц

c₀ = —, c₁ = -^L, ц= ^ц, ⁰ А ¹ А А '

(17)

где

(t, - to)(t? -13) - 2(t? -10)²

^a22 ^(t1 ^t0^)ai2 + ^(t1 ^t0 ^)a12^a02 3^(t1 ^t0^)a02,

^{л r}(t2 -10) (t3 -10) ^л

22

f,3 3

(t1

2

(t? -10) _2

A_c =-b₀

+^b1

\

^b2

^a22 ^a02^a12

^a22 ^a12

02

12

(t2 -12) <sup>л

f</sup> (t2 -12)

^b1 (^(t1 ⁽0 ^)a22 ^a02 ) + ^b2

^(t1 ^- t0<sup>)a

A</sup>c₁ = ^b0

^a22 ^a02^a12

12

02

(t2 -12) <sup>л

(</sup>(t2 -12) (t3 -10) <sup>л

(t</sup>1 ^t0^)a22

+^b1

^Ац = ^b0

-a,

02

12

02

(17a)

(ti - t0)(t3 -13) - 4(t2 -12)²

- b₂

Полученные значения свободных параметров полностью определяют гармоническую задачу Коши второго порядка (12), аппроксимирующую экспериментальный процесс X₀(t). Если в результате решения получено значение р=ю²>0, то процесс аппроксимируется тригонометрическими функциями, а при р<0 - гиперболическими. Случай р=0 с вычислительной точки зрения практически невозможен. Кроме того, он представляет собой вариант задачи Коши не с тремя, а с двумя свободными параметрами, что эквивалентно аппроксимации линейной функцией. Поэтому его следует рассматривать отдельно, и поэтому в формулировке задачи (12) сделано ограничение р.^0.

Теперь, если полученные параметры подставить в интегральное уравнение (13) и вычислить его на исходном процессе X₀(t), то в правой части интегрального уравнения получится новая функция X₁(t), которую мы назвали остатком аппроксимации:

В силу взаимно однозначной обратимости неоднородного интегрального уравнения Вольтерра второго рода и неоднородной дифференциальной задачи Коши, мы получим



В тригонометрическом случае р=ю²>0 общее решение этой задачи имеет вид



а связь между исходным и остаточным процессом получается, если дважды продифференцировать это выражение

t

X₀ (t) = x'' (t) = -OK₁ sinw(t -1₀) - Wx₀ COsw(t -1₀) + X₁ (t) - Wj dT sinw(t - T)X₁ (t). (21)

^t0

Продифференцировав еще раз, получим в результате выражение для аппроксимационной производной

t

Xo'(t) = x'''(t) = -w²x₁ COsffl(t-1₀) + w³x₀ sinO](t-1₀) + X₁'(t)-W jdTCOsffl(t-T)X₁ (t). (22)

^t0

Рассмотрев дифференциальную аппроксимацию процесса X₀(t) с помощью простейшей задачи Коши (12), мы тем самым решили проблему выделения циклических компонент в экспериментальных данных. При этом получен четкий критерий, когда гармоническая составляющая в данных присутствует (р=ю²>0), а когда отсутствует (|Д<0), Естественно, речь идет о данных приведенных к нулевому среднему значению, поскольку гармоническая задача Коши описывает малые колебания около положения равновесия.

Задача выделения циклов, особенно в экономических данных, известна еще с середины XIX века. Так, хорошо известна притча о том, «что семейство Ротшильдов в Европе, работая в обстановке полной секретности, выделило в британских процентных ставках три цикла, включая 40-месячный» [1], что и послужило причиной их обогащения. Немало внимания этой задаче было уделено и в XX столетии.

Саму задачу выделения циклической составляющей из экспериментальных данных в своем классическом виде формулируется в виде вариационного функционала

^t1

J(w,C0,C1) = j dt[X(t) - C0 sin wt - c₁ cos wt]² ^ min. (23)

^t0

Величинами, подлежащими определению, здесь являются не только коэффициенты с0 и с1, но и частота . Включение частоты в состав переменных сразу делает задачу (23) нелинейной и найти ее аналитическое решение в такой постановке невозможно. Численно решить эту задачу, конечно же, можно. Для это, например, можно разбить ее решение на последовательность n линейных задач, пробегая (чаще всего с фиксированным, достаточно мелким шагом Дю) значения частоты из интервала ее определения - ю₀ , Ю₁=Юо+Аю, ... , W_n=W₀+nAw, после чего найти минимальное

значение из полученного набора значений для вариационного функционала J ^ = J(w_k,C0,C1), k = 0,n.

Однако, такой линеаризованный подход к существенно нелинейной задаче, во-первых, требует достаточно большого объема вычислений для полубесконечного частотного интервала, во-вторых, оставляет неисследованными крайние частотные области (0, ю₀) и (w_n, ^), и, в третьих, всегда существует вероятность того, что в следствие все той же нелинейности системы истинный минимум может «провалиться под сетку».

Метод выделения циклической компоненты из экспериментальных данных с помощью дифференциальной аппроксимации, описанный выше, лишен всех этих недостатков. Основное его достоинство в том, что за счет изменения формулировки решать приходится линейную вариационную задачу (17), а не нелинейную (23). Это сразу упрощает жизнь и позволяет найти аналитическое решение, что и было сделано. Кроме того, применив вместо функциональной аппроксимации (23) дифференциальную (17), мы можем предположить, что биржевый процесс, по крайней мере, в самом ближайшем бедующем, будет аппроксимироваться все той же задачей Коши. Это позволит нам, с точностью до остаточного процесса типа белого шума с небольшой энергией (дисперсией), определить бедующее состояние рынка.

Пример практического применения дифференциальной аппроксимации.

Рассмотрим пример практического применения дифференциальной аппроксимации. В качестве экспериментальной функции X(t) возьмем данные об изменении курса британского фунта стерлингов GBP к американскому доллару USD с 16 ноября 1997г. по 24 февраля 2002г. Как было показано в моей работе [2], движение биржевой цены (котировка) может быть разложено на статическую и динамическую составляющие, причем динамика биржевых курсов определяется ценой открытия (сокращенно O - Open) эквидистантного единичного временного интервала. В качестве единичного интервала возьмем неделю. Это даёт сеточную функцию в Т=224 точки. Естественно, интервал определяется лишь тем объемом данных, которые имелся в моем распоряжении на момент написания статьи.

Таким образом, X(t)=GBPUSD.W.O(16.11.97 17:00 NYT; 24.02.02 17:00 NYT). Поясним сделанное символьное сокращение записи. Обозначения подобного рода применяются в программировании при обозначении вложенных структур данных. Биржевые данные имеют именно такую, вложенную, структуру и мне представляются естественным и логичным применять для них аналогичную систему сокращения записи. Верхней структурой здесь является валютная пара GBPUSD, затем следует «уровень времени» (W -Week, неделя), т.е. тот временной интервал, на котором рассматриваются данные и, наконец, тот элемент бара данных (в данном случае точка открытия бара), который непосредственно используется в расчетах. Подобную структурную детализацию можно продолжить вглубь настолько, насколько это представляется необходимым. И последнее, данные, используемые мною, и относятся к Нью-Йоркскому часовому поясу, для которого использую сокращение NYT. В дальнейшем указание на часовой пояс не приводится.

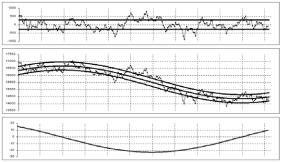
Первая аппроксимация, показанная на рис.1 представляет собой волну с параметрами

x₁₀ =-2186127.42, x₁₁ =-41233.14, ю₁ = 0.01959, T₁ = 321,

(24а)

e₀ = 951.99, e₁ = 288.76, s₁ = e₀/e₁ = 3.297

где Ті - период, и первый индекс нумерует аппроксимации. Исходный сигнал нумеруется индексом 0.

Сам рисунок состоит из трех частей. Средняя часть - основная. На ней отображена экспериментальная функция и ее дифференциальная аппроксимация вместе с каналом, полуширина которого равна энергии e₁ (дисперсии) остаточного процесса X₁(t). Сам же остаточный процесс с тем же каналом отображен в верхней части. В нижней части рисунка отображена аналитическая составляющая аппроксимационной производной (19) без учета остаточного процесса (X₁(t) в этой формуле полагаем равным нулю, чтобы не затушевывать стохастикой регулярную динамику процесса).

Данный пример высвечивает наиболее интересную особенность дифференциальной аппроксимации - период первой гармоники T₁=321 больше, чем количество точек, по которым она строилась, T₁>T. Напомним для сравнения, что в разложении Фурье период основной гармоники равен длине интервала аппроксимации. Поэтому, для каждого следующего момента времени, если не доказана периодичность процесса именно с периодом стартового интервала, разложение Фурье приходится пересчитывать с другим, большим, периодом. При этом спектральные коэффициенты для каждого последующего интервала разложения формально никак не связаны с предыдущими, несмотря на то, что их изменение будет адиабатически слабо меняющимся (достаточно близкими).

Вторая аппроксимация, показанная на рис.2 является результатом выделения чистой гармоники уже из остаточного процесса X₁(T). Параметры этой волны

x₂₀ =-16422.12, x₂₁ = 177.57, w₂ = 0.05514, T₁ = 114,

(24б)

e₁ = 288.76, e₁ = 243.25, s₂ = e₁ / e₂ = 1.186

Дифференциальная аппроксимация динамических экспериментальных (биржевых) данных

Важный вывод, следующий из сравнения (24а) и (24б) состоит в том, что периоды первой и второй гармоник не являются кратными (как в разложении Фурье). Таким образом, полученное разложение (дифференциальная аппроксимация) выделяет последовательность некратных гармоник динамического экспериментального процесса.

С другой стороны, как видно из рис. 2, остаток после второй аппроксимации чисто визуально представляется стационарным стохастическим процессом, не обладающим периодичностью. Дальнейшие аппроксимации в данном временном интервале проводить можно, однако, сжимаемость s при этом существенно не меняется.

Поскольку задача Коши является точечной задачей, наиболее точно описывающей динамику процесса в «малой» окрестности начальной точки t₀, то в результате многократного применения алгоритма дифференциальной аппроксимации на одном и том же отрезке данных, мы получим все более точное приближение, но все более «малой» окрестности начальной точки. В «дальней» зоне, не попадающей в «малую» окрестность, экспериментальный процесс и его дифференциальная аппроксимация будут расходиться все больше и больше. Это свойство зримо наблюдается уже на примере аппроксимации четырьмя гармониками, показанном на рис.3.

Модификация метода.

Такое положение вещей совершенно непригодно для анализа биржевой информации. То, что мы будем знать все точнее и точнее динамику процесса в окрестности некоторой «исторической» точки to, и при этом все хуже и хуже аппроксимируется процесс в окрестности конечной, самой важной, точки текущего момента времени t₁, казалось бы, смазывает практическую ценность данного метода. Однако эта проблема имеет достаточно изящное решение.

Достаточно вспомнить, что задача Коши определяет процесс, развивающийся как в будущее, так и в прошлое. По понятным причинам вторая возможность в практическом плане обычно не рассматривается. В прошлом и так все ясно. Однако, именно эта возможность позволяет переформулировать задачу Коши, выбрав в качестве точки определения «начальных данных» последнюю точку t₁, т.е. точку реального времени. Тогда «малая окрестность» будет формироваться уже вокруг точки t₁, и именно вокруг нее будет хорошо аппроксимироваться экспериментальный динамический процесс. При этом появляется надежда на то, что все последующие данные, пришедшие после момента времени t₁, также будут хорошо описываться данной аппроксимацией, по меньшей мере, до тех пор, пока они попадают в «малую окрестность».



Puc.1 GBPUSD.W.O(16.11.97; 24.02.02) - дифференциальная аппроксимация одной гармоникой.



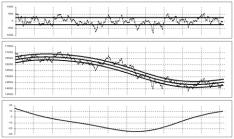
Рис.2 GBPUSD.W.O(16.11.97; 24.02.02) - дифференциальная аппроксимация двумя гармониками.



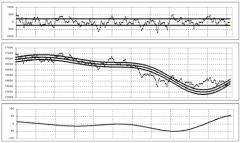
Рис.3 GBPUSD.W.O(16.11.97; 24.02.02) - дифференциальная аппроксимация четырьмя гармониками, отнесенная к начальной

точке интервала.



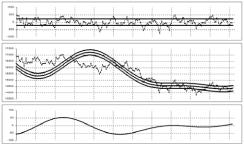
Рис.4 GBPUSD.W.O(16.11.97; 24.02.02) - дифференциальная аппроксимация четырьмя гармониками, отнесенная к конечной

точке интервала.

Как и в предыдущем случае, сопоставим временной процесс X(t) старшей производной и проведем интегрирование:

^x”^(t) = ^X0^(t),

^t1

x^,(t) = ^-J dx ^X0^(t) + x^,(ti⁾,

t

^ti

^x(t) = J^dT(T-t)X0^(т)-x'^(ti^)(ti ^-1) + ^x(ti⁾-

t

Подставив результаты интегрирования в задачу Коши (25), получим интегральное уравнение ti

^X0^(t) +д[^{dT (т-t)X}0^(T) + ^ci^t + ^c0 = ^{0 c}i = M^x,(tiX ^C0 =^^(x(ti^{) - t}i^x'^(ti⁾⁾.

t

Дальнейшее составление вариационной задачи и получение соответствующей ей линейной алгебраической системы третьего порядка для данной модификации метода ничем не отличается от того, как это было сделано в предыдущем случае. Разница будет лишь в определениях коэффициентов системы (I6). Для данного случая ее коэффициентами будут

ti ti ti ti ti А Л

aQ2 = a20 = JdtJdx(x-t^x), a_u=a2i = JdttJdx(x-t)X)(x), a22 = {d1 jdx(x-J(t)

^t0 V<sup>t

t</sup>0 <sup>t

t</sup>0 <sup>t

t</sup>i ^ti ^ti ^ti

b₀ = J dtX ₀(t), b_i = J dtX ₀(t)t, b₂ = J dtX ₀(t) J dт (т- t)X₀(т). (i66)

Используя полученное выше решение алгебраической системы (I7, Па), определим остаток от аппроксимации

^ti

^Xi^(t) = ^X0^(t) + Ц J^{dT(т- t)X}0^(т) + Ci¹ + ^c0, C = ^^x'^(ti⁾, ^c0 = Ц^(x(ti^{) - t}i^x'^(ti⁾⁾.

t

после чего, легко восстанавливается неоднородная задача Коши. Рассмотрим лишь тригонометрический случай р=ю²>0 этой задачи

x”(t) + W²x(t) = Xi(t), x(ti) = x0, x'(ti) = xi. (26)

Точка t_i разбивает временную ось на два полубесконечных интервала - прошлое и будущее. Решения задачи Коши (26) в этих интервалах имеют несколько различающиеся представления и их удобно записать отдельно. Для прошлого (t<t_i) решение задачи Коши (26) и его производные до третьего порядка включительно имеют вид:

X 1 ^tl.

x(t) = - ^sin ш(t₁ - t) + x₀cos w(t₁ - t) + Jdт sin ш(т — t)X₁(т)

ш ш i

^t1

x'(t) = x₁ cos ш(t₁ — t) + x₀шsin ш(t₁ — t) — Jdт cos ш(т — t)X₁(T),

1

X₀ (t) = x'' (t) = x^sin o(t₁ — t)—x^² coso(t₁ — t)+X₁ (t) — шJ dT sin ш(т—t)X₁ (t),

X₀'(t) = x'''(t) = —x^ coso(t₁ — t)—x₀ш³ sino(t₁ — t)+X₁' (t)+Щ² J dT cos<M(T—t)X₁ (t).

Для будущего (t₁<t) решение задачи Коши (26) и его производные до третьего порядка включительно имеют вид (можно сравнить с (20-22)):

X 1 ¹

x(t) = ^sin ш^ — t₁) + x₀ cos ш(t — t₁) + Jdт sin ш^ — т)X₁(т),

ш ш;

Ч

t

x'(t) = x₁ cos ш^ — t₁) — x₀шsin ш(t — t₁) — J dт cos ш^ — т)X₁(т),

t1

t

X₀ (t) = x'' (t) = —x^sin^t—1₁)—x₀o? coso(t—1₁) + X₁ (t) — fflJ dT sino(t — t)X₁ (t),

t1

t

Xo'(t) = x''' (t) = —x₁«² cosn(t—1₁)+x₀nn³ sino(t—1₁)+X₁'(t)—ш² J dT cosn(t—t)X₁ (t).

t1

Естественно, само решение и все выписанные его производные непрерывны в точке текущего времен t1.

В результате модификации задачи Коши, мы получили дифференциальную аппроксимацию, которая по мере увеличения числа гармоник все точнее и точнее описывает процесс в окрестности текущего момента времени. На рис. 4 приведен пример аппроксимации четырьмя гармониками. Видно, что аппроксимация стала практически зеркально-симметричной по отношению к случаю, изображенному на рис.3.

Еще одним положительным моментом модификации метода можно считать то, что при повторении процедуры дифференциальной аппроксимации вовсе не обязательно, чтобы интервал аппроксимации оставался неизменным. Мы можем проводить аппроксимацию на вложенных интервалах, выбирая моменты времени, соответствующие началам интервалов все ближе и ближе к его конечному (текущему) моменту времени. Тем самым у нас уменьшается временной

масштаб аппроксимации. Кроме того, у нас возникает произвол в выборе левой точки интервала, что можно использовать для дополнительной оптимизации аппроксимации. Правда, при этом происходит потеря "дальней" части исторических данных, но это явление достаточно естественное, поскольку мы никогда не знаем (или не пользуемся) всеми историческими данными. Вместо "исторических" данных в нашем распоряжении остаются их дифференциальные аппроксимации крупномасштабными волнами, на фоне которых мы можем, сжимая интервалы аппроксимации к текущему моменту времени все точнее и точнее аппроксимировать исходный динамический экспериментальный процесс.

Заключение.

Изучение любого экспериментального динамического процесса обычно имеет своей конечной целью получение начально-краевой дифференциальной задачи, в рамках которой данный процесс описывается с приемлемой степенью точности. Для большинства реальных процессов в дифференциальной задаче, если даже ее удается построить, присутствуют нелинейные вклады, причем нелинейности могут присутствовать как в уравнениях задачи, так и в ее начальнокраевых условиях. Для динамических задач нелинейности в начальных условиях удается избежать, если перейти к локальному описанию процесса в "малой" окрестности "начального" момента времени. Это так называемая (локальная) задача Коши. Нелинейность в самом дифференциальном уравнении при этом, естественно, остается.

Если предположить только то, что такая нелинейная задача Коши существует, то наша единственная экспериментальная кривая представляет собой траекторию ее точного решения, вышедшего из начальной точки. Саму задачу, по единственно известному решению, мы восстановить (однозначно) не можем. Но мы можем, с помощью метода дифференциальной аппроксимации, в малой окрестности начальной точки (точнее, той точки, которую мы выбрали в качестве начальной, и молчаливо предполагая, что эта точка не является особой) последовательными приближениями линейными задачами Коши с постоянными коэффициентами все более точно описывать неизвестную нам (нелинейную) динамическую задачу. При этом интервал применимости данного метода по мере увеличения числа аппроксимаций становиться все меньше и меньше, стягиваясь к начальной точке. Эта ситуация аналогична разложению функции в ряд Тейлора в окрестности регулярной точки.

В качестве оценки погрешности метода дифференциальной аппроксимации можно принять энергию (норму, дисперсию) выходного процесса. Хотя, возможно, это не самая оптимальная оценка. Заметим, что введение понятия "энергия процесса" позволила объединить математический аппарат функциональной и дифференциальной аппроксимации, как для стохастических, так и для детерминированных процессов в единое целое.

Кроме того, остается открытым вопрос о величине "малого" интервала, в котором справедливы сделанные приближения. Численные расчеты с большим количеством аппроксимаций показывают, что "малая окрестность" гораздо меньше (лишь часть) интервала, на котором проводится аппроксимация.

Начиная писать эту статью в феврале 2002г., я естественно пользовался историческими биржевыми данными, доступными мне в то время. На рис. 1 и 2 видно, что аппроксимационная производная прошла к тому моменту времени нулевую точку и стала строго положительной. Это говорит о том, что рынок перешел в фазу роста. Период второй аппроксимации равен 114 неделям. Стадия роста в чистой гармонике равна половине периода, т.е. 57 неделям, или примерно одному году. Развитие биржевого процесса с февраля по июнь (к моменту окончания работы над статьей) действительно показывает существенный подъем ранка. Так, по Gbp рынок вырос на величину порядка 1000 пунктов (Gbp(24.02.02 17:00)=14318, Gbp(30.06.02 17:00)=15325). Естественно, рост рынка обусловлен объективными экономическими факторами и прогнозу на столь долгий срок не подлежит, тем не менее, можно предположить, что глобальная дифференциальная аппроксимация, как способ приближенного описания динамики системы, все же обладает некими предсказательными возможностями. Как минимум, основываясь на аппроксимационной производной, мы можем определенно сказать, в какой стадии находится рынок, растет или падает, при его одно-, двух- или более кратной гармонической аппроксимации.

Дифференциальную аппроксимацию можно проводить не только линейными задачами Коши с постоянными коэффициентами, но и задачами Коши с переменными коэффициентами. Важно, чтобы при этом можно было бы решить задачу восстановления начальных данных по коэффициентам аппроксимации. В случае, рассмотренном в данной работе, эта задача вырождалась в треугольную алгебраическую систему и решалась элементарно. В других случаях система может иметь достаточно сложный нелинейный вид.

Все вопросы по данной работе, которые бы Вы хотели обсудить с автором, можно прислать мне по e-mail:

Литература.

1. Кравчук В. Поиск трендов и циклов в курсе EUR/USD. // Валютный спекулянт, №2, 2002, с.16-21.

2. Нефёдов Б.Н. Интерполяция бара полиномом третьего порядка. // Экономика и финансы, №2, 2001, с.49-68.

Б.Н. Нефедов





Содержание раздела

---

---

Главная сайта

---