Авдеенко А. - АБСОЛЮТНЫЙ СОВЕТНИК ИЛИ СТОХАСТИЧЕСКИЕ МОДЕЛИ ТОРГОВЛИ
Рассматривается алгоритм торговли на тяжелых хвостах распределения финансовых последовательностей. Устанавливаются критические условия и параметры для реализации беспроигрышного советника. Алгоритм подвергнут тотальному тестированию на рынке Форекс для периодов 1990-2012 гг.
Материал изложен в максимально доступной для не специалистов - математиков форме.
І.Введение
В эконометрике существует большой набор стандартных моделей. Это модели скользящего среднего MA(q), авторегрессии AR(p), смешанные модели, например ARMA(p,q) [1,2]. Эти модели неспособны предсказать динамику условной дисперсии.
Следующее приближение - модели типа ARCH(q), которые представляют условную дисперсию как линейную функцию квадратов прошлых возмущений. В дальнейшем она была обобщена до GARCH(p,q) модели, в которой условная дисперсия в данный момент времени является линейной функцией условной дисперсии и квадратов возмущений в предшествующие моменты времени [3,4].
Модель GARCH можно представить в виде ARMA процесса, определить условия стационарности и использовать для прогнозирования волатильности. Следующее уточнение модели GARCH(p,q) - модель EGARCH(p,q) позволяет учитывать эффекты асимметрии - отрицательную корреляцию между доходностью и волатильностью.
Математические аспекты этих моделей достаточно просты, однако реальное применение при создании автоматизированных торговых систем не слишком эффективно. Нахождение коэффициентов модели может быть реализовано в виде той или иной статистической процедуры или с использованием нейронных сетей, однако при этом практическая реализация приводит к тривиальным результатам - коэффициенты модели либо незначимы в статистическом смысле либо определены недостаточно точно для эффективного принятия решения, например, о входе или выходе в короткую или длинную позицию.
В предлагаемой работе автор пошел по несколько иному пути: анализировалась динамика не условных моментов, а условных вероятностей, причем, не для всех возмущений, а для, так называемых, хвостов распределения - существенных отклонений, доля которых составляет порядка 10-4 ...103 всей последовательности. Данный алгоритм был встроен в модель адаптивного поведения [5-7] и реализован в среде MQL-5.
Ряд наиболее сложных проблем находятся на стыке детерминированного и статистического описания. Где кончается детерминированность и необходим учет статистических свойств системы?
Очень многие важные эффекты лежат вне доступности стандартных статистических процедур: именно, редкие события, а не средние свойства часто определяют поведение системы.
При этом надо естественно оговориться, что редкие событие - это событие все же случающиеся неоднократно, просто их доля в общем количестве событий очень мала. Для редких событий так же возможно использование статистических методов, так называемых статистик хвостов распределений.
2.Модель хвостов распределений
Пусть исходная информация - дискретная финансовая последовательность xn = x (t ) котировка валютной пары в момент времени tn .
Чтобы исключить несущественные колебания (менее спреда) под xn будем понимать взвешенное среднее цен открытия, закрытия, максимума и минимума для заданного таймфрейма, который положим равным минимально возможному т = 1 мин. Введем величину yn = xn+1 xn - изменение xn в процессе эволюции систем.
Величину у будем рассматривать как случайный процесс. В дальнейшей в зависимости от удобства записи случайный процесс у будем записывать как у , либо у (t) , понимая при этом, что мы всегда имеем дело дискретной случайной величиной, определенной лишь в момент времени tn
Единственное, но вполне естественное допущение относительно процесса y (t) - эргодичность, т.е. равенство среднего по ансамблю случайных траекторий среднему по времени.
Более сложно определить стационарность или нестационарность случайной функции (процесса) y(t). С формальной точки зрения стационарность в узком смысле - это независимость n мерной плотности распределения f (y1... yn ) от сдвига во времени t ^ t + T .
Очевидно, что это определяется интервалом рассмотрения функции: для больших интервалов процесс почти стационарен, для малых, естественно, нет. В частности, тренд порождает ненулевой первый момент одноточечной функции распределения, изменение знака тренда - изменение момента и, как следствие, нестационарность процесса.
Кроме того, необходимо учитывать тот факт, что при любом анализе мы имеем дело с выборочными статистиками, а не статистиками генеральной совокупности, т.е. реально имеются выборочные моменты и гистограммы распределения (эмпирические статистики), а не искомые моменты и плотности распределения.
В дальнейшем условимся, что в контексте данной работы, под стационарностью процесса будем понимать неразличимость функций распределения при сдвиге во времени в рамках той или иной статистической гипотезы, принятой или отвергнутой с определенным уровнем риска а .
В частности, удобно использовать непараметрический критерий Колмогорова, который позволяет проверить принадлежность двух выборок {x} {y} к одному распределению. Для этого рассчитывается максимальная разность
двух эмпирических функций распределения Kmax = -JNmax |F(y) F(z)| сравниваемая с табличным значением при заданном уровне риска.
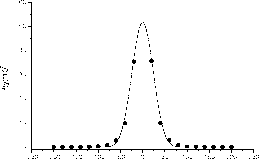
На рис. 1 представлена эмпирическая гистограмма распределения величины y(t) для пары eur/usd за период 2012.
Всего использовано 120000 точек, гистограмма имеет 20 разрядов, величина y (t) одноминутной разности взвешенных средних, для удобства представления оценок, умножена на 105 , т.е. выражена в т.н. единицах Point.
Сдвиги в прошлое на любую величину в интервале от 104 до 3*105 минут с уровнем риска 0.01 по критерию Колмогорова не позволил выявить статистически значимое различие эмпирических распределений. Это позволяет сделать вывод о стационарности рассматриваемого процесса, по крайней мере, в этих масштабах.
Восстановление теоретического распределения можно провести разными способами. Один из вариантов был использован в работе [5] и связан с поиском стационарного решения уравнения Фоккера-Планка.
Однако, существует более очевидный способ, основанный на предложенном Г. Хакеном и др. принципом максимальной информационной энтропии [8].
Согласно этому принципу, при наличии эмпирических ограничений - моментов порядка к: ук
стационарное распределение имеет вид f (у) = exp(-(Л0 + Ау + Ау2 + ¦¦¦Лкук )) , где Лк множители Лагранжа
(фактически, константы модели), для определения которых можно использовать метод градиентного поиска или, так называемую, эволюционную стратегию.
Опуская простые подробности можно показать, что метод сводится к системе уравнений
А =в(gk - ук ) (1)
где gk - среднее по искомой функции распределения, тем самым, зависящее от всех Ак ; ук среднее по распределению, задаваемому системой, т.е. эмпирическое среднее, в константа, определяющая скорость релаксации.
Штрих над величиной Ак - это производная по времени релаксации, т.е. разница между двумя последующими приближениями Ак . Величины gk определяются численным интегрированием или с использованием теории возмущений, например, в виде диаграммной техники. Множитель А0 определяется из условий нормировки.
Не представляет труда построить многоточечные функции распределения, например, f (yn+1, yn) В этом случае в качестве внешних ограничений можно воспользоваться двухточечными корреляционными функциями Уп +1 Уп ¦
Гораздо больший интерес представляют так называемые условные плотности распределения, например,
f ( Уп + 1, Уп , Уп-і)
f ( Уп _1)
двухточечная условная плотность f (уп+1, yп |yn_1)
Эта функция характеризует совместное распределение случайных величин yn+1, yп при условии, что значение Уп_1 задано. Алгоритм аналогичен использованному выше, но в этом случае множители Лагранжа зависят от величины у , ¦ п_1
Используя алгоритм (1), была построена негауссовская аппроксимация или теоретическое распределение колебаний валютного курса пары EUR/USD - сплошная линия на рис.1.
Выбиралась модель четной степени относительно y , не выше четвертого порядка, т.е. внешними 2 4 ограничениями служили эмпирические моменты y , y
Соответствующие величины составили Л2 = 8.67 - 10 4 ,Л4 = _1.9 - 10 8. Отсюда можно сразу оценить амплитуду колебания с существенно негауссовой составляющей или, так называемые, тяжелые хвосты
распределений yc= 2 что составляет приблизительно 214 единиц в принятой системе координат или 2.14 10-3 в абсолютных значениях.
Иными словами, изменение курса более чем на 0.2 процента в течении минуты связано с существенной негауссовской составляющей. Это хвосты распределений, для которых существенны нелинейные эффекты.
Однако, абсолютная доля хвостов в общей последовательности невелика (5-15)* 10-5 или, в среднем, от 2 до 5 всплесков в месяц.
Именно эти хвосты распределений и алгоритмы торговли на них и будут рассматриваться в дальнейшем.
Пусть 8 - торговый спред. Введем условные вероятности Р , Р_ следующим образом
Р+ = Р (Уп+1 + Уп 8^ Уп 8 Уп-1): Уп-1 0 =Р- = Р (- Уп+1 - Уп 8^- уп 8 уп _і): Уп-1 0
Смысл этих величин очевиден это вероятности того, что при заданном положительном или отрицательных скачках уп-1 в момент времени tn-1 скачок уп в момент времени tп или в момент времени tn+1 превысит величину спреда. Если условные вероятности f (уп+1, уп|уп-1) синтезированы с помощью алгоритма (1), то процесс вычисления очевиден.
Например,
8 +^ 8 +^
Рис.1 Гистограмма распределения ( о ) величины и ее аппроксимация моделью (1)
У Р+ = 1 - j f (Уп + Уп +1 , Упп + | Уп-1 )dуп +1 j аУп j f (Уп + Уп +1 , Упп +1 Уп-1 )dУп j dyr.
Естественно, что в этом случае вероятности P+, Р_ функции переменной yn-1 выражаемые через
зависимости Р+,Р_ в нужном порядке малости по Р+_ = а1+_yn_1 + а+_уП_1 +....
На рис.2 и 3 по отдельности для различных знаков yn_1 представлены зависимости условных эмпирических вероятностей Р+, Р_ от величины yn_1 - символы (| ) и теоретическая аппроксимация полиномами не выше второго порядка по yn_1 .
Р+= 0.53yn_і _0.0014у2_і Р_=_0.85yn_і _0.0022у2_і
Рис.2 Условная вероятность Р+ в зависимости от изменения взвешенного среднего y для случая y0; таймфрейм 1 мин., пара EUR/USD, 2012
Рис.3 Условная вероятность P- в зависимости от изменения взвешенного среднего у для случая y0; таймфрейм 1 мин., пара EUR/USD, 2012
Графики и соотношения (2) представляют существенный интерес для торговли на хвостах распределения. Действительно, если предшествующее изменение мало, то вероятность того, что оно сохранит знак и превысит спред менее половины, при изменениях более 100-120 единиц, вероятность достигает 0.65 ..0.70 и, наконец, при сверхбольших скачках вновь становится более вероятным изменение знака.
Можно сделать оценки условий, при которых максимальна вероятность сохранения направления движения а - и сверхбольшой амплитуды, при которой P ^ 0 :
2а+- - а1 + YC валютного курса
Соответствующие величины в принятом масштабе составляют 189-193 и 378-376 единиц соответственно для положительного и отрицательного скачков валютного курса. Оценка Y+max
близка к соответствующей оценке амплитуды негауссовой составляющей, вычисленной ранее.
Отсюда сразу же возможна оценка прибыльности алгоритма торговли на хвостах, именно превышение количества прибыльных трейдов за время N0 равно N = N0 P1 (2Pmax 1) , где P1 вероятность наблюдать скачок max max
соответствующий максимуму Y+ , P+ максимальное значение условной вероятности.
Подставляя соответствующие величины из гистограммы и соотношений (2), имеем
Pi =(5-15)*10-5 , Pmax =0.65...0.67 или N = N0 - (1.5...5) - 10 5, что соответствует 1.3 трейдам в месяц или 12 .36 в год.
Соответствующий программный блок, реализующий этот алгоритм в общей схеме, изображен на рис. 4 в фигурных скобках.
Он может функционировать как отдельно от остального алгоритма, так и вместе, включая вариант мультивалютной торговли.
Рис. 4 Блок-схема алгоритма адаптивного поведения и блока торговли на хвостах распределения: M- модель, C1,2 -контроллеры, X(t) - входной сигнал, Y(t) - смоделированное будущее, Б^)-интегральное управление контроллера 1, К(і)-решение модели адаптивного поведения [2], Бф-решение для хвостовраспределения.
3. Тестирование алгоритма
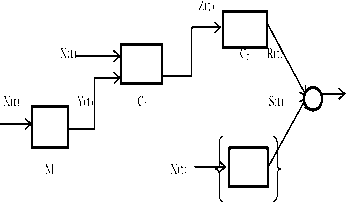
Алгоритм торговли на хвостах распределения был подвергнут тотальному тестированию на паре eur/usd с таймфреймом 1 мин для различных периодов времени. Поскольку оценка числа (не вероятности!) успешных трейдов дает величину 12-36 трейдов в год, то выбирались большие интервалы тестирования от 6 месяцев до пяти и более лет. Алгоритм тестировался отдельно от других блоков адаптивного поведения, представленных на рис.4
В частности, рассматривался пятилетний интервал 1995-2000 гг., двенадцатилетний 2000-2012 гг. и пять двухлетних интервалов с 2000 по 2008 гг. Кроме того генерировались случайные интервалы продолжительностью 6 мес. с 2000 по 2012 гг.
Часть результатов приведены в табл. КИсходный баланс составлял $10000.
Оценивалась суммарная прибыль, число трейдов и просадка при различных уровнях риска от 0.05 до 0.10 и от 0.05 до 0.20. В данном алгоритме связь уровней риска с моделью была опосредованная: уровень риска определял величину лота в зависимости от успешности предшествующих торгов, являясь некоторой функцией уровня свободной маржи, и не влиял на критерии входа - выхода в короткие или длинные позиции.
Не было установлено ни одного убыточного периода продолжительностью свыше 6 мес. Хотя для периодов от двух лет и более максимальная просадка достигала 20 процентов от конечной прибыли.
Число трейдов колебалось от 4 д 22 в год, что близко к априорным оценкам.
Наиболее эффективным оказался период 2010-2012 гг. Последнее, возможно, связано с тем, что для ускорения тестирования константы рассчитывались однократно только для 2012 г. С другой стороны, это свидетельствует об устойчивости предложенного алгоритма и, главное, о стационарности процесса в рассматриваемых масштабах.
Наконец, в конце таблицы представлены результаты тестирования советника на периоде 22 года с 1990 по 2012 гг. В последнем столбце в скобках указана среднегодовая прибыль для различных уровней риска.
Среднее количество трейдов в год вновь порядка 10. Прибыль в зависимости от уровня риска составляет от 970 до 10820 процентов или 11.4 и 23.8 процента в год.
Малое число трейдов определялось самой структурой алгоритма и являлось следствием малого числа существенных (критических) отклонений. Однако, алгоритм практически безошибочно распознавал большие скачки и принимал, почти всегда, адекватное решение.
Алгоритм наиболее предпочтителен для крупных инвесторов, для которых стабильность важнее прибыльности.
4. Нелинейные эффекты в других масштабах
Тяжелые хвосты распределения изменений котировок валютных пар существуют во все масштабах описания, т.е при все значениях интервала предварительного сглаживания. С формальной точки зрения это можно показать с помощью континуального интегрирования по промежуточным состояниям интеграла по траекториям - решения соответствующего уравнения Фоккера-Планка [ 3 ] .
Однако, в прикладном аспекте (предмете предлагаемой статьи), достаточно рассмотреть условные вероятности тех или иных состояний при заданном значении амплитуд предшествующих состояний и на этой основе реализовать поправки к торговой стратегии.
Итак, пусть xn = x(t ) - взвешенно среднее с периодом p1 открытия, закрытия, минимума и максимума
котировок соответствующей валютной пары с таймфреймом 1 мин. Соответственно yn - ее изменение с интервалом p1 .
Введем условную вероятность P (yn +1 yn 0|| yn , p1) сохранения знака yn + 1 изменений при заданном
предшествующем значении модуля |yn| и периоде усреднения p1
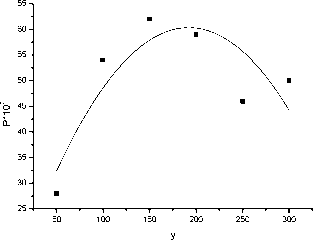
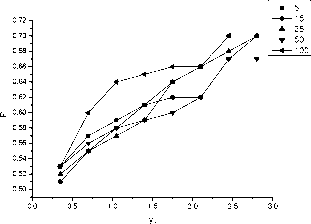
Соответствующие эмпирические зависимости для пары eur/usd за период 2012 при различных значениях p1 представлены на рис.5
Величина yn для удобства представления в одном масштабе нормированы на эмпирическую дисперсию
1N
Л2 = 1 2
1 N1
V y2 с шагом p, на базе N .точек y ^ y / Д
N1 -1 k 1 Уп Уп
Рис. 5 Зависимость условной вероятности сохранения знака изменения величины сглаженных котировок от амплитуды предшествующих значений для пары eur/usd при различных значениях для 2012 года.
Если амплитуда предшествующего состояния близка к 0.5, то вероятность сохранения знака близка к половине, иными словами, как увеличение, так и уменьшение котировки равновероятно, однако при у0 1 существенно более вероятным становится сохранение знака, т.е. продолжение тенденции.
Естественно, при этом доля реализаций таких состоянии резко уменьшается и составляет порядка 104-103 . В масштабах усреднений P1 1 не обнаружено обратной тенденции, которая имело место при P1 = 1 рис. 2 ,3 те снижения вероятности сохранения знака при слишком большой величине у0 .
Точнее, в ряде случаев это наблюдалось для некоторых периодов P1, но количество реализаций подобных состояний было слишком мало даже на годовом интервале наблюдения, поэтому не позволяет пока сделать статистически значимых выводов.
Полученный результат справедлив для любых масштабов усреднения и может считаться, по-видимому, фундаментальным законом для финансовых последовательностей, именно: вероятность сохранения знака изменения финансовой последовательности нарастает практически линейно с увеличение амплитуды предшествующего состояния при у0 1 для любых интервалов предварительного усреднения.
Эти дополнительные эффекты были учтены в блоке контроллера полной модели адаптивного поведения рис. 4. Иными словами, вход в короткую или длинную позицию был обусловлен не только принятием решения адаптивного поведения в контроллере C1 , но и выполнение условия \уп\ ac . Соответствующее тестирование полного алгоритма было проведено на паре eur/usd за период 2012 года.
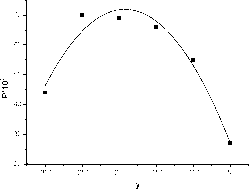
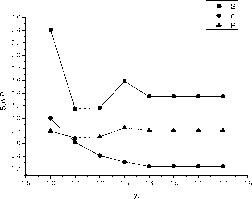
Результаты представлены на рис.6.
Для удобства представления результатов общее число трейдов было поделено на максимальное значение той величины, которое составило 21. Кроме того, полагалось, что величина лота постоянна L=3, в отличие от тестирования по алгоритму только хвостов, в которых L определялась в зависимости от величины свободных средств и составляла в среднем 0.5-0.8 стандартного лота в $100000.
Исходный баланс, как и прежде, составлял $10000.
Рис. 6. Суммарная прибыль S, количество трейдов п, и вероятность P прибыльного трейда в зависимости от амплитуды предшествующего состояния. С ростом величины \у п\ на графике она обозначена у 0 несколько увеличивается вероятность прибыльных
трейдов, но снижается их общее число, которое остается неизменным при у0 1.4, что соответствует
отключению полного алгоритма и работе его части, связанной только с торговлей на хвостах с минимальным периодом усреднения, т.е частью алгоритма тестирование, которого отражено в табл.1.
5. Дискуссия и перспективы
Термин абсолютный советник использованный в названии статьи носит, естественно, условный характер и означает, что вероятность безубыточной торговли S 0 стремится к единице при неограниченном увеличении интервала функционирования советника при условии стационарности функции распределения: P (S 0, N0 ^ 1 если
Последнее неизбежно для длинных последовательностей. Более того, наличие так называемых тяжелых хвостов распределения и делает, по-видимому, возможным реализацию подобного алгоритма. Более того, по-видимому, наличие тяжелых хвостов позволяет реализовать алгоритм мультивалютного хеджирования рисков.
Этому будет посвящена следующая работа.
Интересно заметить, что если в исходной задаче сместить начало отсчета на у c отрицательных у , построить для них условное математическое ожидание уи+1 УпУп и аппроксимировать его, по аналогии с (1), полиномом не выше второго порядка, то в континуальном пределе получим уравнение ёу 2
Ланжевена: = аху + а2у + / , где у/ - нормально распределенная дельта - коррелированная случайная dt величина, а1 0,а2 0 .
Интегрирование соответствующего уравнения Фоккера-П ланка дает стационарное решение в виде бимодального распределения с неустойчивой нулевой точкой, характерное для многих физических моделей - от спонтанного вырождения симметрии в квантовой физике до триггерных режимов в социальных и биологических системах.
