Чеботарев Ю. - Еще раз о прогнозе финансового рынка и принципах построения торговой системы
Дискуссия о прогнозах финансового рынка длится давно. И ругательств по этому поводу высказано предостаточное количество.
Дело доходит даже до того, что некоторые исследователи утверждают будто прогнозы это исключительно задача математики. Может быть, с точки зрения математики, и можно обосновать прогноз, как логический процесс. Но, уж никак нельзя говорить, что прогноз вытекает из математики. Скорее следует говорить, что прогноз является элементом дедуктивного анализа.
Вот и рассмотрим возможности прогнозирования с позиций логики.
Для исследования любого явления требуется знать:
(1) исходные, конкретные условия (например, исходные условия существования некоторого процесса);
(2) конечные, конкретные условия (например, результаты исследуемого процесса);
(3) универсально верные обобщения (например, фундаментальные законы). Комбинация набора обобщений с известными исходными условиями дает прогноз. Комбинируя прогноз с известными конечными условиями, получаем:
(4) объяснения (или результаты анализа). Сопоставление известных исходных условий с известными конечными условиями дает возможность провести:
(5) тестирование соответствующих обобщений.
Легко заметить, что существует симметрия между прогнозами и объяснениями. Эти понятия можно логически переставить местами.
Процесс исследования явлений имеет два условных требования. Первое из них анализ явления по 5-ти пунктам возможен только в том случае, когда исследователи явления не могут влиять на это явление.
Другими словами, исследуемое явление протекает во времени вне зависимости от наблюдателей. Второе условное требование.
Исходные и конечные условия, исследуемого явления, должны состоять из фактов, подающихся наблюдению и управляемые универсальными законами.
Например, движение шара по наклонной плоскости. Исходные условия начальная точка движения в момент t = 0. Конечные условия конечная точка движения в момент t. Процесс управляется законами Ньютона. Комбинация исходных условий и силы гравитации дает возможность прогнозировать нахождение шара в любой момент t. Можно провести анализ движения шара не во времени, а в пространстве, сопоставляя временной прогноз с конечными условиями.
Налицо симметрия между прогнозом движения шара и точкой его нахождения в момент t. Процесс движения шара из начальной точки в конечную можно повторить, протестировав, таким образом, действие сил гравитации.
Теперь рассмотрим аналогичный пример движения шара по наклонной плоскости, но с участием наблюдателя. Назовем наблюдателя мыслящим участником процесса, потому что наблюдатель может оказывать воздействие на движение шара исходя из индивидуальных желаний, предпочтений или ожиданий. Шар, из начальной точки наклонной плоскости, начинает движение под действием силы гравитации. В любой момент t мыслящий участник начинает воздействовать на шар по своему желанию может остановить шар или притормозить его, а может направить шар в противоположном направлении.
В результате воздействий мыслящего участника нарушается симметрия между прогнозом движения шара и результатами его нахождения во времени и пространстве. Ассимметрия между прогнозом и объяснением исследуемого явления приводит к невозможности тестирования этого явления.
Таким образом, обобщения не применимы к будущему в той же степени, в какой они применимы к прошлому.
Таким образом, симметрия между объяснением и прогнозом существует только при отсутствии мыслящих участников. В противном случае прогнозы всегда будут обусловлены желаниями, предпочтениями и ожиданиями участников процесса.
Такие процессы не могут обладать законченностью.
Если приведенные выше примеры достаточно просты по своей структуре, то структура финансового рынка призывает к детализации. Для простоты изложения будем понимать под финансовым рынком совокупность из трех рынков валютного, товарного и фондового. Участниками финансового рынка являются компании производители, компании обслуживающие производителей, перерабатывающие компании, сервисные компании, финансовые институты, фонды, частные инвесторы, спекулянты, хеджеры и т.д. Финансовому рынку присущи две характерные особенности.
Первая из них финансовый рынок ничего не производит, он только перераспределяет активы. Вторая все участники финансового рынка действуют независимо друг от друга. Уже тот факт, что количество участников крайне велико говорит о невозможности какой-либо зависимости между участниками рынка. Большинство торгуемых активов на финансовом рынке обладают высокой ликвидностью.
Например, ведущие мировые валюты на валютном рынке, фьючерсы на энергоносители на товарном рынке, акции голубых фишек на фондовом рынке.
Непреложными фактами финансового рынка являются:
¦ финансовый рынок состоит из активов самих участников рынка;
¦ составной частью финансового рынка являются мыслящие участники, количество которых крайне велико, и они принимают свои решения о перераспределении активов независимо друг от друга.
Перейдем к рассмотрению общего механизма функционирования финансового рынка. Для этого рассмотрим два понятия фундаментальная ценность актива и рыночная стоимость актива. Фундаментальная ценность актива определяется в зависимости от способности актива давать доход.
Богатства компаний, как участников финансового рынка, устанавливают фундаментальную ценность ее активов. На фундаментальную ценность активов напрямую оказывают влияние прибыли и дивиденды компании, движение наличности в компании, слияние и приобретение компаний, переход в открытую форму или в закрытую форму, рейтинг кредитоспособности, доверие участников финансового рынка к активам самой компании. Рыночная стоимость актива определяется индивидуально каждым участником рынка в зависимости от спроса и предложения на этот актив на рынке.
Фундаментальная ценность актива является полезным руководством при принятии решений об инвестициях для участников рынка. Процесс инвестиций протекает путем обмена активов, принадлежащих участникам рынка, на активы самого рынка, но уже по рыночной цене. В любом случае считается, что в течение небольшого отрезка времени рыночная стоимость активов стремится к фундаментальной ценности активов. На рынке действует огромное количество участников, взгляды которых, как правило, различаются.
На финансовом рынке желания и предпочтения участников выражаются в покупках и продажах активов. При прочих равных условиях позитивные предпочтения к фундаментальным ценностям актива ведут к росту котировок на этот актив, а негативные к их падению.
Рассмотрим абстрактный пример. Обозначим стоимость одного из активов на финансовом рынке через рі? где z = 1, ¦¦¦ _ предположим, что на некотором отрезке времени наблюдается
равновесие между рыночной стоимостью и фундаментальной ценностью актива. На этом отрезке времени значение цены актива Р| = const t 0.
Мыслящие участники финансового рынка руководствуются в своих дуйствиях ожиданиями, предпочтениями и желаниями. Если на рынке складывается ситуация, когда фундаментальная ценность i-го актива растет (или может вырасти), то этот эффект выражается в росте котировок i-го актива. Изменения в котировках, в свою очередь, влияют на превалирующее предпочтение участников рынка.
В результате роста котировок i-го актива, растет рыночная стоимость этого актива. А тенденция роста на определенном временном отрезке формирует тренд, где Pi t const
t 0.
Предпочтения и ожидания участников финансового рынка всегда различны потому, что, во-первых, носят ярко выраженный индивидуальный характер, и во-вторых, представляют собой случайную совокупность желаний независимых участников финансового рынка. Сказать, как долго продлится тренд на определенном временном отрезке, нельзя потому, что продолжительность и глубина этого тренда зависит от совокупности случайных ожиданий и предпочтений независимых участников рынка. Отрезок времени, где формируется тренд может быть большим и маленьким. Тренд может зародиться и тут же умереть, а может и наоборот продлиться достаточно длительное время.
Все характеристики тренда управляются совокупностью случайных ожиданий и предпочтений независимых участников финансового рынка. Уже сама природа формирования тренда на финансовом рынке говорит о том, что невозможно никакое прогнозирование этого явления.
Потому, что налицо ассимметрия между прогнозами рынка и результатами случайных предпочтений участников рынка.
Такая совокупность случайных ожиданий и предпочтений участников финансового рынка сильно напоминает процесс броуновского движения. Полное определение этого процесса относится к физике.
Дадим характеристику броуновского движения так, как это сделано в физике.
Броуновским движением называется непрерывное хаотическое движение частиц. Причиной броуновского движения частиц являются различные импульсы со стороны других частиц.
В силу хаотичности движения, частица в любой момент времени испытывает неуравновешенное воздействие, которое непрерывно изменяется по направлению и величине. В результате этого частица находится в беспорядочном движении.
Характеристикой броуновского движения является средняя величина квадрата смещения частицы в произвольном направлении х2. Из-за хаотичности броуновского движения среднее смещение частицы х = 0, ибо частица с равной вероятностью может двигаться в противоположных направлениях. При этом х2 t 0.
Закономерности броуновского движения:
¦ Броуновское движение продолжается неограниченно долго, без каких либо видимых изменений.
~2
. Величина х не зависит от внутренних свойств частицы.
~2
. Значение х возрастает только под действием внешних факторов.
Если отсутствует воздействие внешних факторов, то х2 = const t 0 . При наличии внешнего
воздействия х2 t const t 0. Например, если некий объем газа находится под постоянными
давлением и температурой, то воздействие внешних факторов отсутствует и х2 = const t 0 . Если на объем газа произвести направленное воздействие путем увеличения температуры, то
х2 t const t 0, поскольку не зависит от внутренних свойств частицы. Усложним этот пример. Температура, воздействующая на газ, имеет тенденцию постоянного увеличения на каком-то
отрезке времени. Действие температуры приведет к формированию тенденции роста х2 на этом отрезке времени.
Надо полагать, что читатель уже увидел адекватность между природой броуновского движения и поведением цен на активы финансового рынка. Конечно, говорить о полной адекватности броуновского движения и поведения цен на рынке еще рано.
Аналогия между этими явлениями имеет важное методологическое значение для построения торговой системы. А именно, в основе торговой системы должны лежать следующие принципы:
¦ финансовые рынки не прогнозируются;
. поведение цен на активы следует рассматривать, как хаос, который управляется совокупностью случайных ожиданий и предпочтений независимых участников рынка.
Большинство читателей, пожалуй, согласится с тем, что торговая система, построенная на таких принципах, заведомо обречена на успех. Какими бы сложными и удивительными не казались эти принципы, построить торговую систему на их основе оказалось делом возможным.
Создана не одна такая система, и не одним автором.
Хаос как объект спекулятивного обогащения
Как же зарабатывать на финансовом рынке, который подобен броуновскому движению? За броуновским процессом можно наблюдать со стороны.
А можно посмотреть на финансовый хаос, как участник рынка. На рынке торгуется большое количество активов. Обозначим і-й финансовый актив через fj, где г = 1, ¦¦¦ . как показано выше, желания и предпочтения
участников рынка делают недостижимым состояние равновесия рынка на длительном отрезке времени. Случайные желания и предпочтения участников рынка постоянно сдвигают процесс от равновесия.
Это как частица в броуновском движении, на которую воздействуют импульсы со стороны других движущихся частиц. В результате, целью процесса становится не достижение равновесия, а некая желаемая и предпочтительная стоимость актива, которую легко представить в виде движущейся мишени.
Рассмотрим абстрактный пример, который прояснит нам конструкцию торговой системы. Финансовый рынок представим себе в виде большого количества движущихся мишеней.
Каждая i-я мишень есть ^-й финансовый актив. Отдельного участника рынка, под которым
можно понимать инвестора, спекулянта или трейдера, представим в роли стрелка. Основная задача стрелка сводится к отстрелу мишеней, которые могут принести прибыль.
На мишени высвечиваются цифры стоимость i-го актива pr Цифры эти постоянно меняются. Все мишени
одного цвета белого. Но в какой-то момент времени мишень может менять цвет на красный или зеленый. Под сменой цвета понимается следующее.
Есть некий механизм, который сигнализирует, что по текущей цене Pi можно войти в рынок с длинной позицией. В этом случае
мишень становится зеленого цвета. Если некий механизм сигнализирует, что по цене Pi можно войти в рынок с короткой позицией, то мишень окрашивается в красный цвет.
Таким образом, перед стрелком движется огромное количество мишеней. Мишени белого цвета периодически меняют цвет на зеленый, или красный.
На мишени постоянно высвечивается цифра стоимости актива Pi. Стрелок может поразить мишень и заплатить стоимость мишени p в
момент поражения. После поражения мишени, ее передают стрелку. Пораженная мишень находится у стрелка до тех пор, пока цвет мишени не поменяется на противоположный от того цвета, когда мишень поразили.
Если мишень поразили при зеленом цвете, то при появлении красного цвета мишень желательно вернуть туда, где движутся все мишени. За возвращение мишени стрелку отдают стоимость мишени Pi в момент возврата. Другими словами, если при
зеленом цвете мишени мы поразили i-ю мишень по цене Pibuy, то при красном цвете мы
вернули эту мишень по цене PjSel1. Разница (PjSel1 - Pibuy) есть результат стрельбы по мишени.
Понятно, что стрельба по мишеням проводится не бесплатно. У стрелка должны быть доступные (cash value) средства D для поражения мишеней.
Результаты стрельбы по i-й мишени не обязательно должны быть положительными. Отрицательные результаты стрельбы приводят к уменьшению доступных средств стрелка.
Введем понятие предельно допустимой просадки доступных средств стрелка P. Обычно эта величина выражается в относительных единицах измерения. Учитывая, что стрелок может поражать большое количество мишеней в пределах доступных в текущий момент средств D, величину P можно выразить следующим образом:
я
-Р
При внимательном рассмотрении, представленное неравенство есть ни что иное, как функционал управления рисками стрелка. Такой функционал однозначно идентифицирует успешного стрелка (winner) от неудачного стрелка (loSer).
Так, как же стать успешным стрелком? Для этого требуется сделать анализ функционала управления рисками. Но, первоначально рассмотрим еще один, наводящий, пример с бросанием монеты.
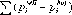
Будем считать появление орла на монете выигрышем, а появление решки проигрышем. Когда мы бросаем одну монету, вероятность выигрыша 0,5.
Понятно, что при бросании монеты неограниченное количество раз, когда I со, наш выигрыш будет равен нулю. Теперь представим, что имеется некий механизм, который позволяет изменить вероятность появления орла -? в сторону увеличения, а вероятность появления решки -q в сторону уменьшения так, что ? + q = 1. Очевидно, что наличие такого механизма дает возможность при t * со стабильно быть в выигрыше.
Вернемся к стрелку и его движущимся мишеням. Пример с монетой и некий механизм заработка нужен был для понимания следующей аналогии.
Когда перед стрелком движутся мишени и i-я мишень меняет цвет с белого на зеленый, стрелок получает сигнал на возможный отстрел этой мишени по цене Pjbuy. Поразив i-ю мишень, стрелок не знает, сможет ли он
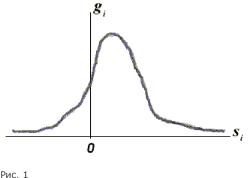
получить выигрыш, вернув мишень обратно по цене PjSel1. (Инвестор не знает этого потому, что финансовые рынки не прогнозируются). Обозначим через Vj вероятность появления события Sj = (PjSel1 - Pjbuy), а через gj плотность распределения вероятности Vj (см.рис.1).
(Заметим, что создание такого механизма возможно обычными методами современного технического анализа.)
Из функционала управления рисками вытекает второе правило успешного стрелка. Чем больше доступных средств у стрелка, тем меньше просадка этих средств, а следовательно и меньше риски.
Аналогичные выводы можно получить из тривиальной задачки теории вероятностей о разорении игрока. (Не будем обсуждать эту задачу подробно, а отошлем читателя к учебнику по теории вероятностей.) Итак, второе правило успешного стрелка: отстрел мишеней стрелок должен делать с достаточно большим запасом доступных средств.
Прибыль стрелка определяется суммой
Успешный стрелок это прибыльный стрелок.
Как уже говорилось выше, стрелок, поразив мишень по цене pjbuy, не знает будет ли прибыльная эта мишень. Очевидно, что сумма і-і будет иметь
положительную тенденцию роста только в том случае, если количество поражаемых мишеней n будет достаточно большим. Положительная тенденция роста, при достаточно большом п, будет
0 а 1 gi dsi 1 Si dsi
(На языке финансового рынка это называется диверсификация активов.) Третье правило успешного стрелка: стрелок не должен ограничивать себя количеством поражаемых мишеней. Он должен стремиться к тому, чтобы в любой момент времени у него было как можно большее количество пораженных мишеней. (Другими словами, трейдер должен вести активный процесс купли-продажи финансовых активов с их глубокой диверсификацией.)
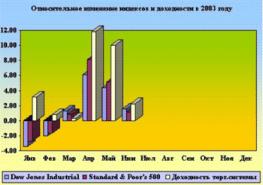
Торговая система, построенная по правилам успешного стрелка, применяется автором на американском фондовом рынке. Результаты работы этой торговой системы ежедневно публикуются на сайте.
Можно сравнить результаты доходности торговой системы по месяцам с относительным изменением биржевых индексов за это же время (см. рис.2).
