Запись линеаризованных уравнений в стандартных для ТАУ формах

Представим линеаризованное уравнение (*) в форме уравнения движения и в виде ПФ.

Уравнение движения предполагает: а) выходную величину и ее производные в левой части уравнения, а входную и все остальные члены - в правой; б) так же, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Чтобы привести линеаризованное уравнение (*) к такому виду введем обозначения:

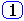
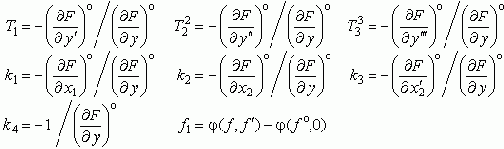
тогда:

T33Dy''' + T22Dy'' + T1Dy' + Dy = k1Dx1 + k2Dx2 + k3Dx'2 + k4 f1 .

Знак D обычно опускают и записывают уравнение в символьном виде:

(**)

(T33 p3 + T22 p2 + T1 p + 1) y = k1Dx1 + (k2 + k3 p) x2 + k4 f1 ,

где:  
 
 

T3, T2, T1 - постоянные времени;
k4, k3, k2, k1 - коэффициенты усиления;
p=d.../dt - оператор дифференцирования.

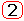
y = W1(p) Dx1 + W2(p) x2 + Wf (p)  f1 ,

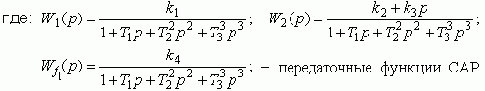
Более строго передаточные функции определяются через изображения Лапласа или Карсона-Хевисайда, как отношение изображений выходной и входной величин: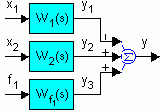

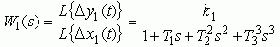
Запись ПФ для переменных во времени величин и для их изображений совпадает до оператора. В первом случае ПФ зависит от оператора дифференцирования p=d.../dt. Во втором случае - от оператора Лапласа s=c+jw.

Содержание раздела

---