(1)
Tdy/dt + y = K x(t) .
Уравнение соответствующего звена с запаздыванием t будет иметь вид:
(2)
T dy/dt + y = K x(t-t) .
Оно называется дифференциально-разностным.
Обозначим x*(t) = x(t-t), тогда уравнение (2) запишется в обыкновенном виде:
(3)
T dy/dt + y = K x*(t) .
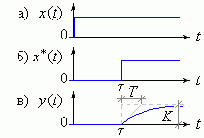
Следовательно его переходная характеристика соответствует апериодическому звену (Рисунок 1в), но задержана на t с, что определено задержкой воздействия x*(t) (Рисунок 1б).
Резюме:
- Временная характеристика любого звена с запаздыванием будет такая же, как у соответствующего обыкновенного звена, но только сдвинута по оси времени вправо на величину t.
- Величину запаздывания t в звене можно определить экспериментально, путем снятия временной характеристики.
