При компьютерном моделировании существенными следует считать только три источника погрешности:
- Трансцендентные функции, которые вычисляются компьютером путем аппроксимации полиномиальными или степенными рядами:
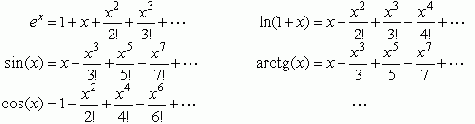
- Дискретный квазианалог интегратора (блок 1/S).
- Итерационный решатель (тот или иной классический алгоритм, предназначенный для решения алгебраических уравнений путем подбора независимых переменных до заданной точности).
Погрешности дискретных квазианалогов интеграторов играют решающую роль в компьютерном моделировании. На рисунке показано, как дискретный квазианалог интегратора (блок 1/S) обрабатывает сигнал синусоидальной формы. Наглядно видно, что при уменьшении шага симуляции погрешность интегрирования дискретным квазианалогом интегратора снижается. Это основное правило, которому надо следовать при настройке параметров симуляции.
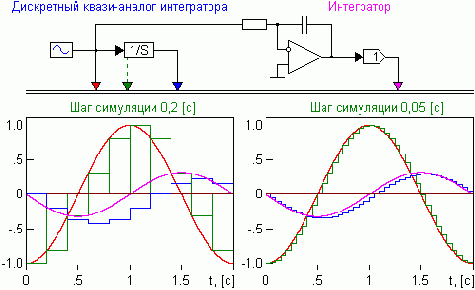
Очевидно, что разные методы дискретного интегрирования будут иметь разные величины погрешности. Эту погрешность лучше представить в виде декомпозиции на амплитудную и фазовую составляющие и оценивать их величины в частотном домене. Максимальное влияние проявляется от фазовой погрешности.
Простейшая модель синусоидального генератора на двух интеграторах позволяет убедиться в том, что погрешности всех классических методов интегрирования лежат в том диапазоне, который определен двумя методами Эйлера с запаздыванием и с упреждением. Таким образом при выборе шага симуляции следует уменьшать его до тех пор, пока вариация переходного процесса (от переключения упомянутых методов) не будет укладываться в заданный допуск.

Переходные процессы в системе, вызваны ненулевыми начальными условиями. Частотная характеристика разомкнутой системы очевидна (-40дБ/дек. & -180°). Методу Эйлера с запаздыванием соответствует расходящийся переходный процесс; методу Эйлера с упреждением – сходящийся; методу трапеций – синусоида с постоянной амплитудой
