Пусть имеем характеристическое уравнение:
a0 s n + a1 s n-1 + ... + an-1 s + an = 0 .
Приведем его к нормированному виду (разделим на an и выполним подстановку
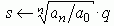
q n + a1/an (W0 q) n-1 + ... + ak/an (W0 q) n-k +...+ 1 = 0 ,
где: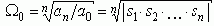
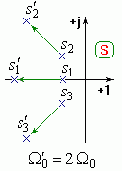
Для приведенного уравнения время будет безразмерным t = W0 t, переходная функция h(t) в случае кратных вещественных корней или одной пары комплексных будет ограничена минорантой и мажорантой:
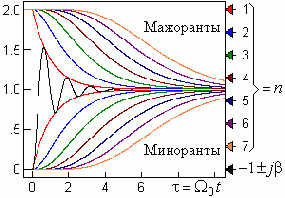
где: u(h, t) = e -ht [1 + (ht)1/1! + (ht)2/2! + ... + (ht)n-1/(n-1)! ] - разложение в ряд Тейлора огибающей той составляющей в пререходном процессе, корень которой ближе к оси "+j".
На Рисунок демонстрируется, что любой переходный процесс в любой системе будет затухать тем медленней, чем больше корней вблизи оси "+j".
